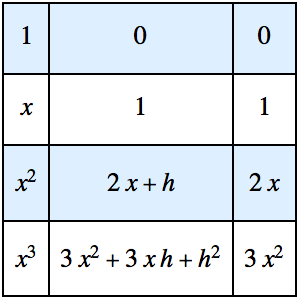
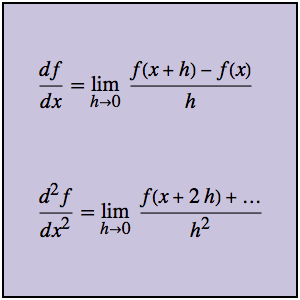Оценка производной с использованием первых принципов
Отношения разностей могут непосредственно использоваться для нахождения не только производной первого порядка, но и производных более высокого порядка. Для начала рассмотрим функцию g и связанное с ней отношение разностей.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
Использование предела отношения разностей даёт производную первого порядка.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
Производная второго порядка может быть вычислена напрямую от второго отношения разностей без ссылки на производную первого порядка.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
Предел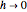 
- это производная второго порядка.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
Отношение разностей производной первого порядка является функцией, отличной от отношения разностей второго порядка g, но его предел также является производной второго порядка.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
