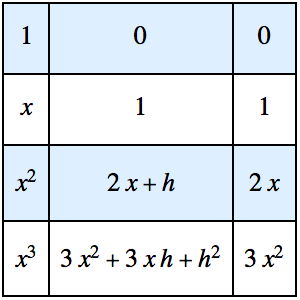
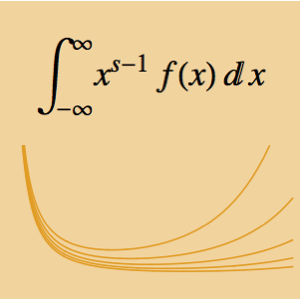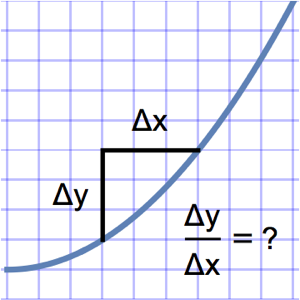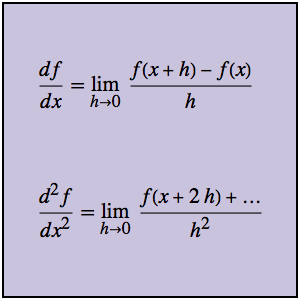Resolva o problema tautocrônico
O problema tautocrônico requer encontrar a curva onde um objeto colocado em qualquer ponto de partida deslizará até seu ponto mínimo gastando o mesmo tempo. Expressando o tempo total de queda em termos do comprimento do arco da curva e a velocidade 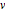 obtemos a equação integral de Abel
obtemos a equação integral de Abel 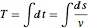 . Definindo a função desconhecida
. Definindo a função desconhecida 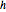 pela relação
pela relação 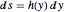 e usando a equação de conservação de energia
e usando a equação de conservação de energia 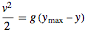 obtemos a seguinte equação explícita.
obtemos a seguinte equação explícita.
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Use DSolveValue para resolver a equação integral.
dsdy = DSolveValue[abeleqn, h[y], y]Usando a relação  , resolva
, resolva 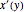 .
.
dxdy = Sqrt[dsdy^2 - 1]Iniciando a curva da origem e integrando obtemos 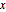 como a função de
como a função de 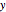 . Note que as suposições asseguram que o integrando tenha um valor real.
. Note que as suposições asseguram que o integrando tenha um valor real.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]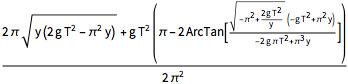
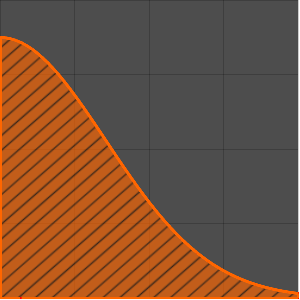
Usando um tempo de descida de dois segundos e substituindo no valor da aceleração gravitacional, faça um gráfico da curva máxima para a tautocrônica. (A parte 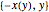 vem da solução
vem da solução 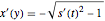 para a derivada de
para a derivada de 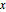 .)
.)
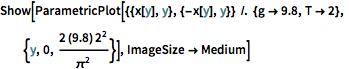
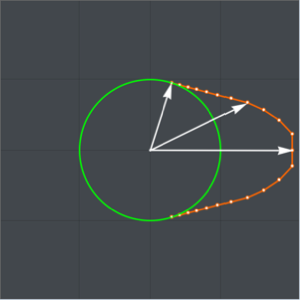
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]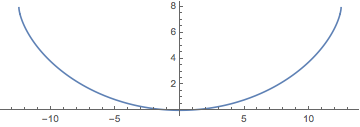
Mudando as variáveis 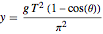 dá uma parametrização simples, não singular da curva
dá uma parametrização simples, não singular da curva 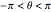 .
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Combinando a equação de conservação de energia e a regra de cadeia 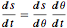 resulta a seguinte equação diferencial para
resulta a seguinte equação diferencial para 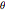 como uma função de
como uma função de 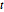 , que pode ser resolvida numéricamente.
, que pode ser resolvida numéricamente.
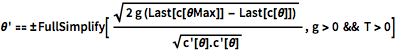
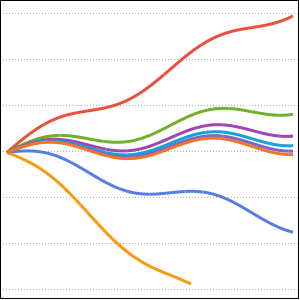
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]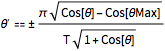
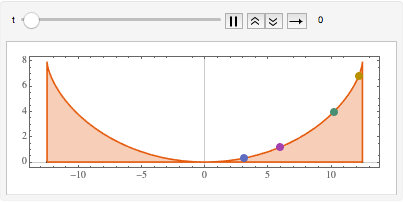
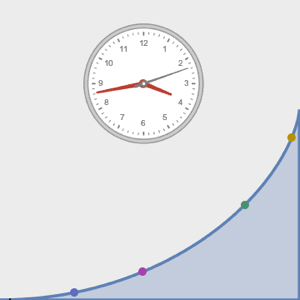
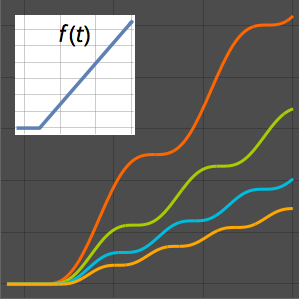
Visualize o movimento ao longo da tautocrônica.