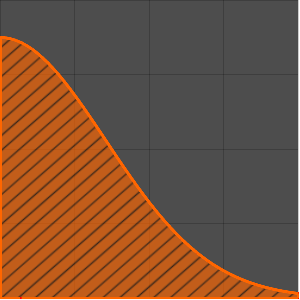
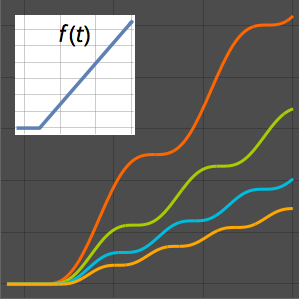
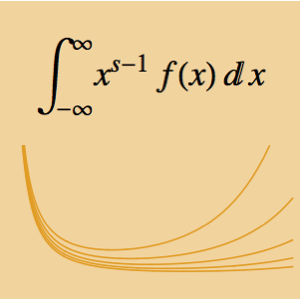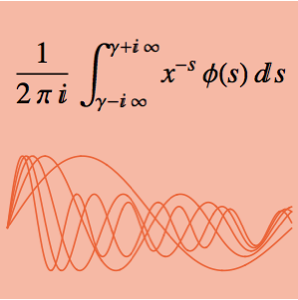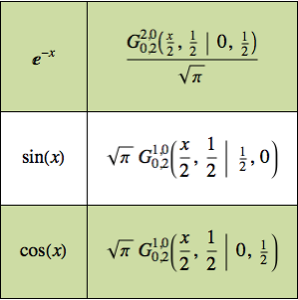Otimize o formato de um came
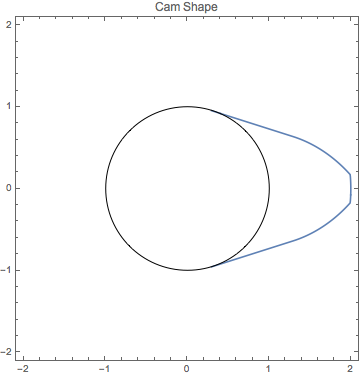
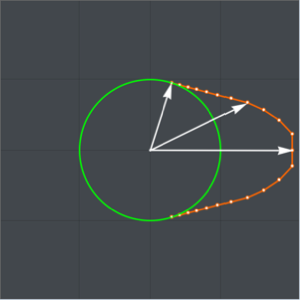
Projete o formato de um came convexo para maximizar a área de abertura da válvula para uma rotação do came, com restrições no raio do came.
Considere que o formato do came é circular em um ângulo de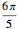 
de sua circunferência com raio 
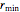e é desenhado simetricamente sobre o restante 
.
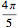As variáveis de design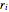 
, 
, 
, 
, 
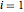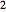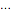, representam o raio do came em ângulos equidistantes 
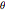distrubidos sobre um ângulo de 
, a metade superior da parte não circular do came.
n = 100; vars = Array[r, n];Cada raio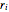 
está restringido para ficar no intervalo 
.
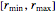rmin = 1; rmax = 2;
varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];Insira o ângulo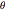 
definido acima.
\[Theta] = 2 Pi/(5 (n + 1));Restrições de convexidade são expressos pelo sistema de desigualdades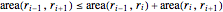 
.
convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <=
(1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[
i + 1] Sin[\[Theta]];Usando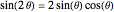 
, o sistema pode ser expressado novamente conforme abaixo. Note que 
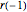é o raio de um ponto na parte circular do came e portanto igual a 
.
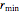convexconstr =
Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <=
r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin,
r[0] -> rmin, r[n + 1] -> rmax};Uma restrição no índice de mudançado raio é expressada em termos do parêmetro α como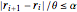 
.
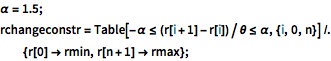
\[Alpha] = 1.5; rchangeconstr =
Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0,
n}] /. {r[0] -> rmin, r[n + 1] -> rmax};A função objetiva (área de abertura da válvula), é esperada que tenha uma relação linear simples com as variáveis de design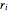 
dadas como 
, onde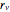 
é uma constante relacionada com a geometria da válvula.
rv = 1;
objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];Escolha os pontos iniciais para as variáveis.
initpts = Table[.5 (rmin + rmax), {i, 1, n}];Resolva o problema de maximização.
sol = FindMaximum[
Join[{objfun}, varbounds, convexconstr, rchangeconstr],
Thread[vars, initpts]];Observe que vários dos raios maiores estão no máximo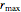 
.
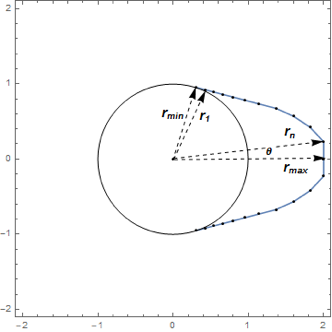
Table[r[i], {i, 95, 100}] /. sol[[2]]
Faça uma representação gráfica da solução.
