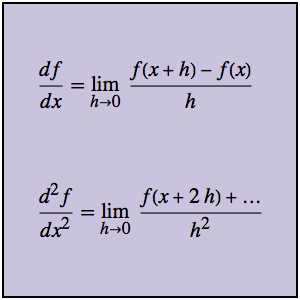第一原理を使って導関数を評価する
差分商は，一次導関数だけでなく高次の導関数を直接計算するためにも使うことができる．まず関数 g とそれに関連した差分商を考える．
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
差分商の極限を取ると，一次導関数が与えられる．
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
二次導関数は，一次導関数を参照しなくても二次差分商から直接計算することができる．
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
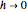のときの極限が二次導関数である．
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
一次導関数の差分商は g の二次差分商とは異なる関数であるが，その極限は二次導関数でもある．
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
