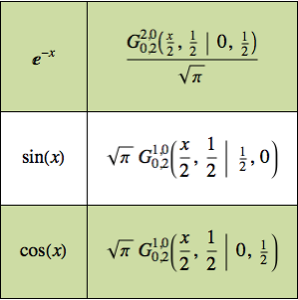Resolva um problema de valor sobre o contorno usando a função de Green

Resolva a seguinte equação diferencial de segunda ordem sujeita a condições de contorno homogeneas.

In[1]:=

eqn = -u''[x] - u'[x] + 6 u[x] == f[x];

In[2]:=

bc0 = u[0] == 0;

In[3]:=

bc1 = u[1] == 0;

O termo forçado vem dado pela função seguinte f[x].

In[4]:=

f[x_] := E^(-a x)

Calcule a função de Green para o operador diferencial correspondente.

In[5]:=

gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]

Out[5]=

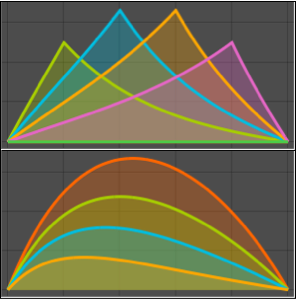
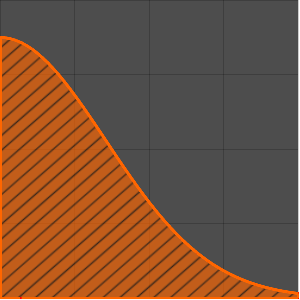
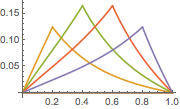
Faça um gráfico da função de Green para diferentes valores de 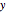que estão entre 0 e 1.

In[6]:=

Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]

Out[6]=

A solução da equação diferencial original com o dado termo forçado pode agora ser calculado usando a integral de convolução no intervalo .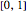

In[7]:=

sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] // Simplify

Out[7]=

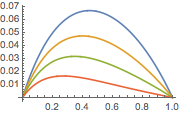
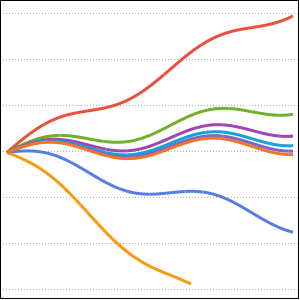
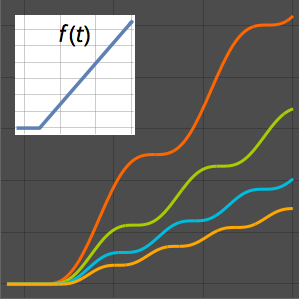
Faça um gráfico da solução para diferentes valores do parâmetro .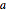

In[8]:=

Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]

Out[8]=