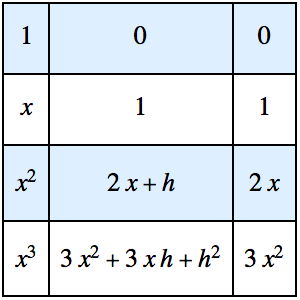
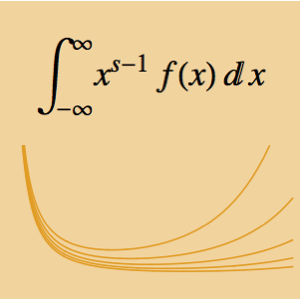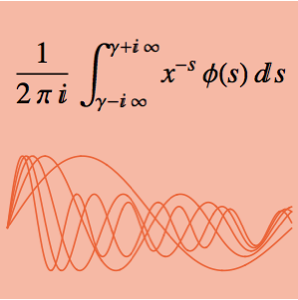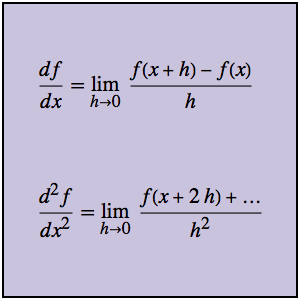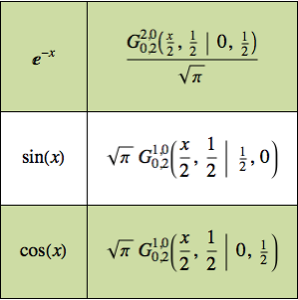Calcule integrais definidas usando redução G: Novos Recursos do Wolfram Language 11

Calcule integrais definidas usando redução G

Expressar funções em termos de MeijerG permite o cálculo de seu produto sobre reais positivos.

Crie uma regra para expressar a integral de um produto de funções em termos de funções de MeijerG.

In[1]:=

IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] :=
  IntegrateMeijerG[
  MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]

Esta integral pode ser expressada exatamente em termos de uma única expressão de MeijerG.

In[2]:=

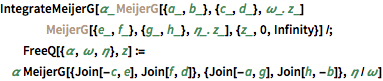
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_, 
      d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_, 
      h_}, \[Eta]_. z_], {z_, 0, Infinity}] /; 
  FreeQ[{\[Alpha], \[Omega], \[Eta]}, 
   z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g], 
    Join[h, -b]}, \[Eta]/\[Omega]]

Use o esquema para calcular .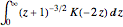

In[3]:=

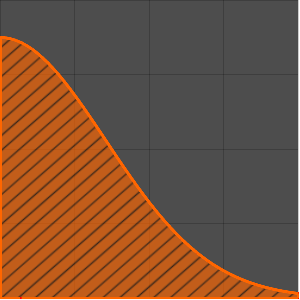
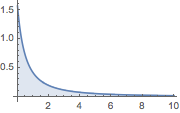
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis, 
 PlotRange -> All]

Out[3]=

In[4]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[4]=

Obtenha o mesmo resultado usando Integrate.

In[5]:=

Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[5]=

Apesar da resposta parecer muito diferente, ela é equivalente.

In[6]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
FullSimplify[% == %%]

Out[6]=