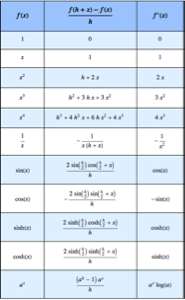
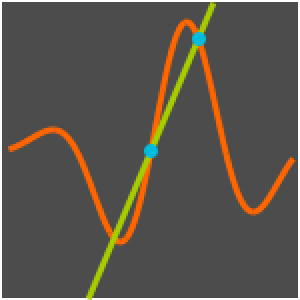
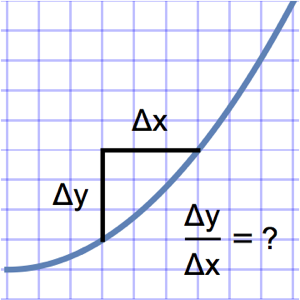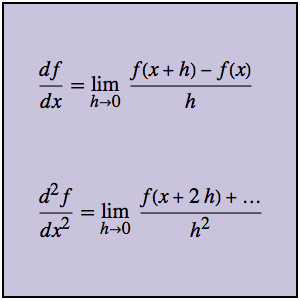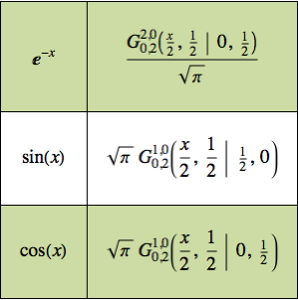Finden Sie die Impulsantwort eines Schaltkreises
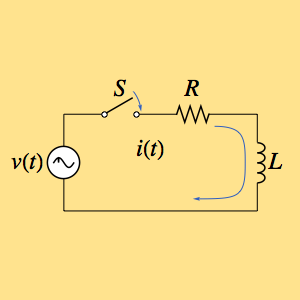
Ermitteln Sie die Impulsantwort eines Schaltkreises, der aus einem Widerstand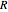 
und einer Spule 
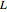besteht und von einer zeitabhängigen Spannung 
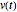angetrieben wird.
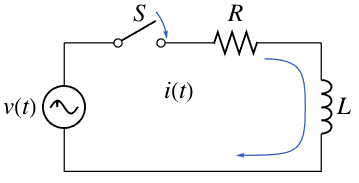
Der Strom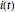 
kann durch das Lösen einer linearen Differentialgleichung erster Ordnung berechnet werden.
Legen Sie den Differentialoperator fest, der zur linken Seite der ODE gehört.
In[1]:=
voltage = L i'[t] + R i[t];Gehen Sie aus von der Annahme, dass die Schaltung anfänglich offen ist.
In[2]:=
init = i[0] == 0;Berechnen Sie die Impulsantwort für den Schaltkreis mithilfe von GreenFunction.
In[3]:=
gf[s_, t_] =
GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]Out[3]=
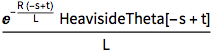
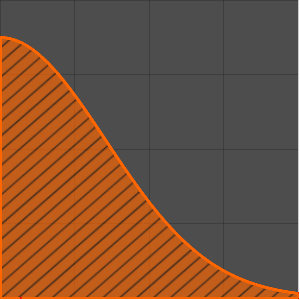
Plotten Sie die Impulsantwort bei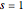 
.
In[4]:=
Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7},
PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]Out[4]=
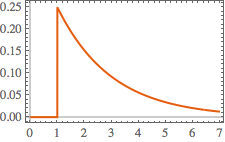
Berechnen Sie die Antwort des Schaltkreises auf eine Spannungsstufe.
In[5]:=
v[t_] := HeavisideTheta[t];In[6]:=
current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]Out[6]=
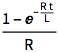
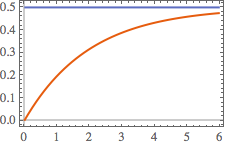
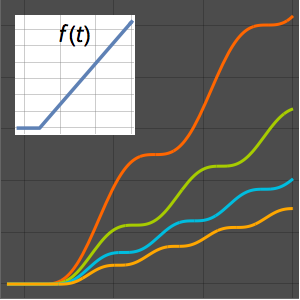
Visualisieren Sie die Stufenantwort.
In[7]:=
Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6},
PlotTheme -> "Scientific"]Out[7]=
