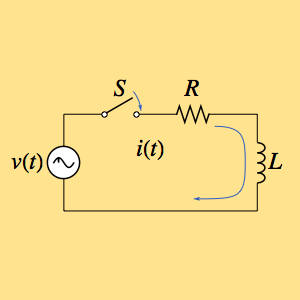
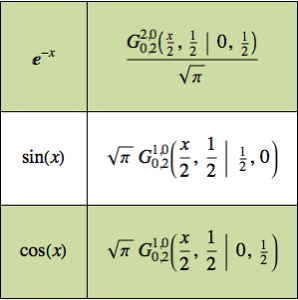回路のインパルス応答を求める

抵抗 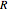とインダクタ 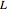からなり，時間依存電圧 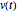によって駆動する回路のインパルス応答を求める．

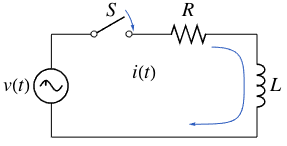
電流 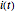は一階線形微分方程式 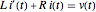を解くことにより計算することができる．

常微分方程式の左辺に対応する微分演算子を設定する．

In[1]:=

voltage = L i'[t] + R i[t];

スイッチは最初は開いていると仮定する．

In[2]:=

init = i[0] == 0;

GreenFunctionを使って回路のインパルス応答を計算する．

In[3]:=

gf[s_, t_] = GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]

Out[3]=

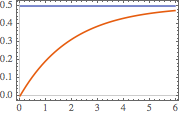
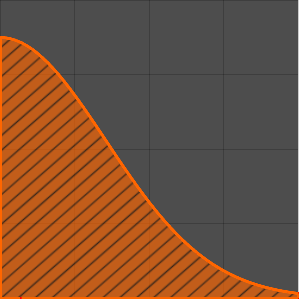
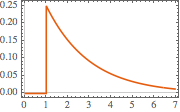
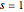におけるインパルス応答をプロットする．

In[4]:=

Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7}, PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]

Out[4]=

ステップ電圧に対する回路の応答を計算する．

In[5]:=

v[t_] := HeavisideTheta[t];

In[6]:=

current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]

Out[6]=

ステップ応答を可視化する．

In[7]:=

Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6}, PlotTheme -> "Scientific"]

Out[7]=