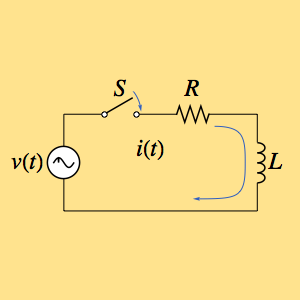
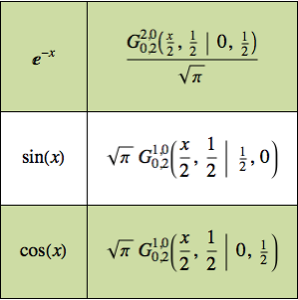Ache a resposta de impulso de um circuito
Encontre a resposta de impulso para um circuito composto por um resistor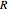 
e um indutor 
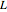, que é acionado por uma voltagem 
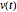depentende de tempo.
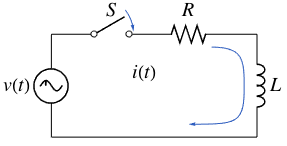
O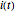 
atual pode ser calculado resolvendo uma equação diferencial linear de primeira ordem 
.
Determine o operador diferencial correspondente ao lado esquerdo da equação diferencial ordinária.
In[1]:=
voltage = L i'[t] + R i[t];Suponha que o interruptor esteja aberto inicialmente.
In[2]:=
init = i[0] == 0;Calcule a resposta de impulso para o circuito usando GreenFunction.
In[3]:=
gf[s_, t_] =
GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]Out[3]=
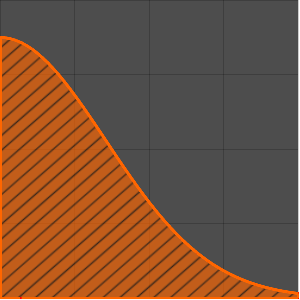
Faça um gráfico da resposta de impulso em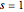 
.
In[4]:=
Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7},
PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]Out[4]=
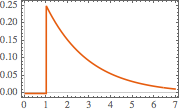
Calcule a resposta do circuito sob a aplicação de uma tensão descontínua.
In[5]:=
v[t_] := HeavisideTheta[t];In[6]:=
current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]Out[6]=
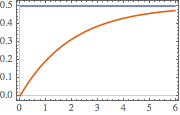
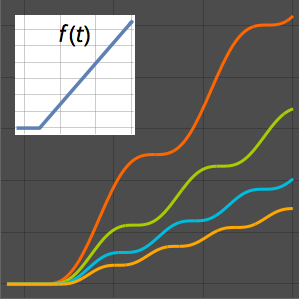
Visualize a resposta.
In[7]:=
Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6},
PlotTheme -> "Scientific"]Out[7]=
