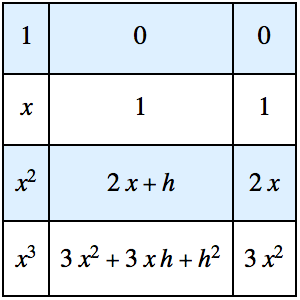
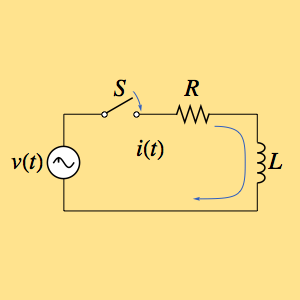
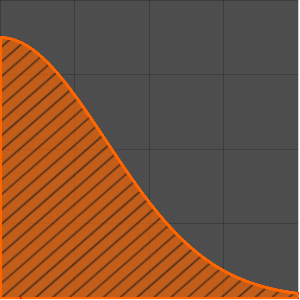
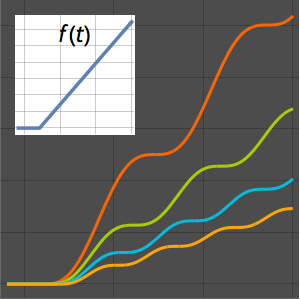
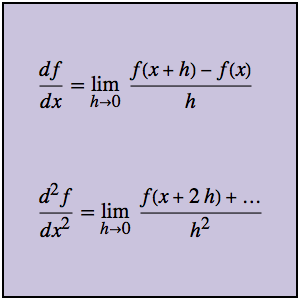求电路的冲击响应
求一个由时变电压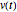 
驱动的，由一个电阻 
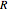和一个电感 
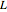组成的电路的冲击响应.
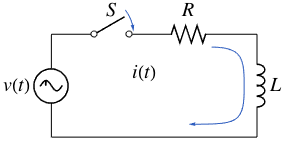
电流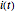 
可以通过求解一阶线性微分方程 
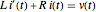来计算.
根据常微分方程的左边设立微分算子.
In[1]:=
voltage = L i'[t] + R i[t];假定开关最初是断开的.
In[2]:=
init = i[0] == 0;用 GreenFunction 计算电路的冲击响应.
In[3]:=
gf[s_, t_] =
GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]Out[3]=
绘制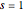 
时冲击响应的图形.
In[4]:=
Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7},
PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]Out[4]=
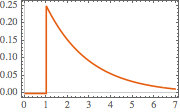
计算电路对一个阶跃电压的响应.
In[5]:=
v[t_] := HeavisideTheta[t];In[6]:=
current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]Out[6]=
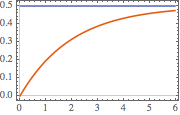
图示阶跃响应.
In[7]:=
Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6},
PlotTheme -> "Scientific"]Out[7]=
