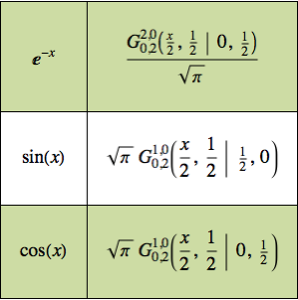Trouvez la réponse impulsionnelle d'un circuit

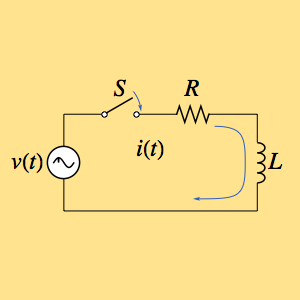
Trouvez la réponse impulsionnelle d'un circuit composé d'une résistance 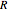et une inductance 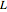, et est entraîné par une tension dépendant du temps .

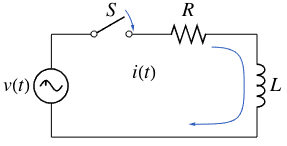
Le courant peut être calculé en résolvant une équation différentielle linéaire du premier ordre .

Configurez l'opérateur différentiel correspondant au côté gauche de l'EDO.

In[1]:=

voltage = L i'[t] + R i[t];

Supposez que l'interrupteur est ouvert initialement.

In[2]:=

init = i[0] == 0;

Calculez la réponse impulsionnelle pour le circuit en utilisant GreenFunction.

In[3]:=

gf[s_, t_] = GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]

Out[3]=

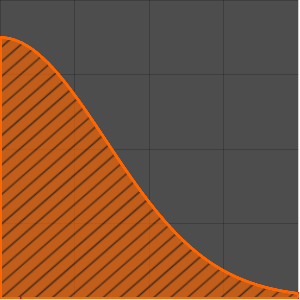
Tracez la réponse impulsionnelle en .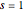

In[4]:=

Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7}, PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]

Out[4]=

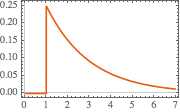
Calculez la réponse du circuit à une tension d'étape.

In[5]:=

v[t_] := HeavisideTheta[t];

In[6]:=

current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]

Out[6]=

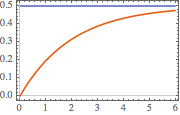
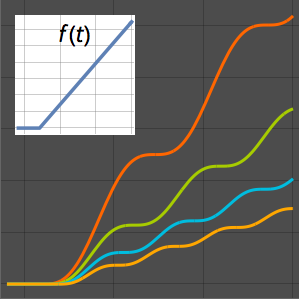
Visualisez la réponse d'étape.

In[7]:=

Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6}, PlotTheme -> "Scientific"]

Out[7]=