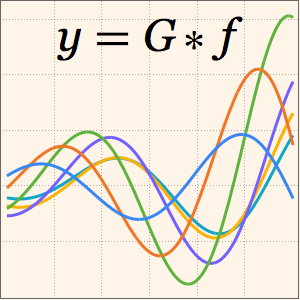Solve an Initial Value Problem Using a Green's Function

Solve an initial value problem for an inhomogeneous differential equation using GreenFunction.

First, compute the Green's function.

In[1]:=

gf[s_, t_] = GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0}, u[t], {t, 0, \[Infinity]}, s]

Out[1]=

Define a forcing function.

In[2]:=

f[t_] := Cos[a t]

Convolving the Green's function with the forcing function yields the solution.

In[3]:=

sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]}, Assumptions -> t > 0]

Out[3]=

Compare with the result given by DSolveValue.

In[4]:=

DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0, u'[0] == 0}, u[t], t] // FullSimplify

Out[4]=

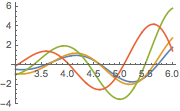
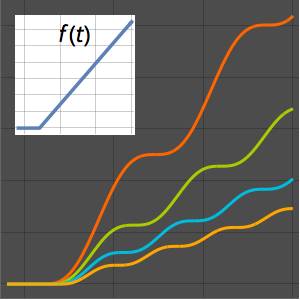
Plot the solution for different values of the parameter .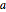

In[5]:=

Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]

Out[5]=