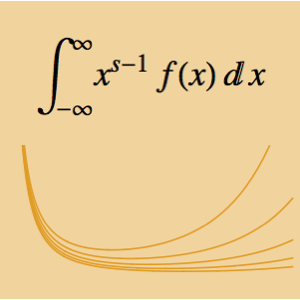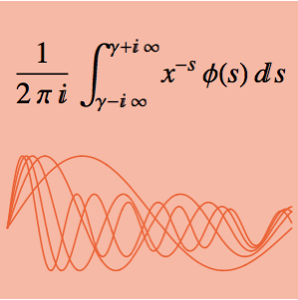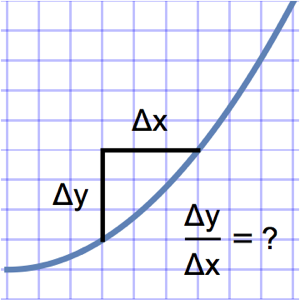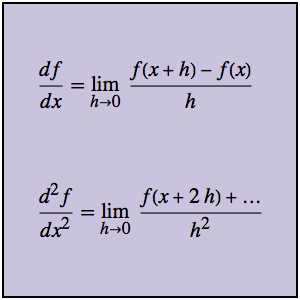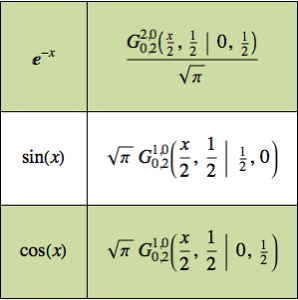等時曲線問題を解く
等時曲線問題では,曲線の任意の場所に置かれたビーズがすべて同じ時間で底まで落ちる,そのような曲線を見付けることが必要となる.曲線の弧長と速度 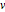 について合計の落下時間を表すと,アーベル(Abel)積分方程式
について合計の落下時間を表すと,アーベル(Abel)積分方程式 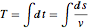 になる.関係
になる.関係 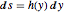 によって未知の関数
によって未知の関数 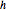 を定義し,エネルギー保存方程式
を定義し,エネルギー保存方程式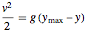 を使うと,以下の明示的な方程式になる.
を使うと,以下の明示的な方程式になる.
In[1]:=
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);DSolveValueを使って,積分方程式を解く.
In[2]:=
dsdy = DSolveValue[abeleqn, h[y], y]Out[2]=
関係 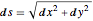 を使って
を使って 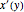 について解く.
について解く.
In[3]:=
dxdy = Sqrt[dsdy^2 - 1]Out[3]=
曲線を原点から開始し積分すると,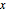 が
が 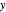 の関数ととして得られる.連想は,被積分関数が実数値であることを確実にすることに注目のこと.
の関数ととして得られる.連想は,被積分関数が実数値であることを確実にすることに注目のこと.
In[4]:=
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]Out[4]=
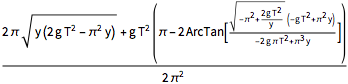
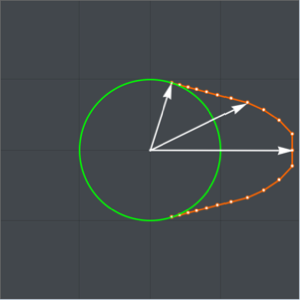
2秒の下降時間を使い,重力加速度の値に代入して,等時曲線の最大曲線をプロットする(分岐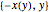 は
は 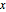 の導関数に対する解
の導関数に対する解 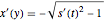 に由来する).
に由来する).
In[5]:=
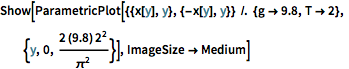
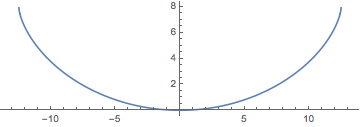
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]Out[5]=
変数 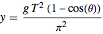 を変化させると,
を変化させると,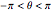 における単純で非特異な曲線のパラメータ化を与える.
における単純で非特異な曲線のパラメータ化を与える.
In[6]:=
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;エネルギー保存方程式と連鎖律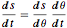 を組み合せると,
を組み合せると,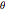 を
を 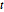 の関数とした以下の微分方程式が生成される.これは数値的に解くことができる.
の関数とした以下の微分方程式が生成される.これは数値的に解くことができる.
In[7]:=
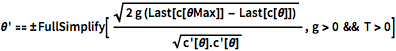
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]Out[7]=
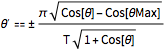
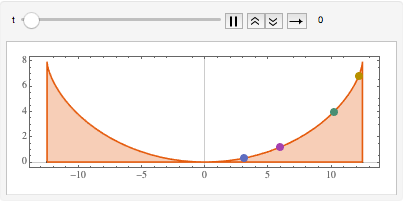
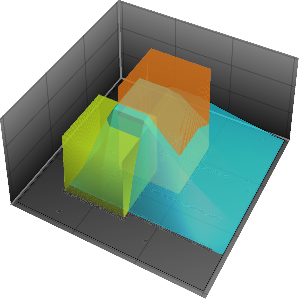
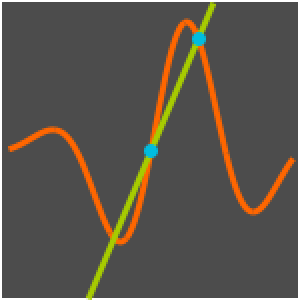
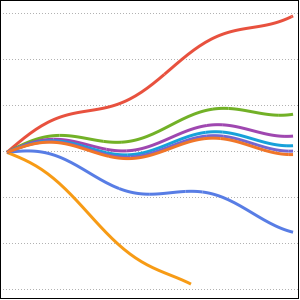
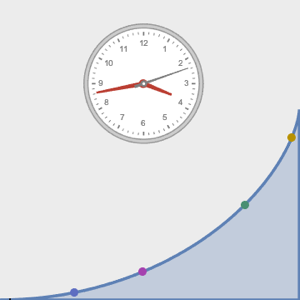
等時曲線に沿った運動を可視化する.