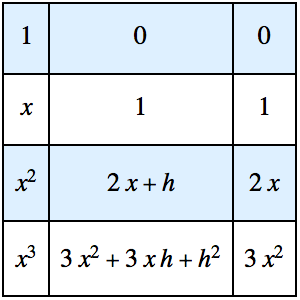
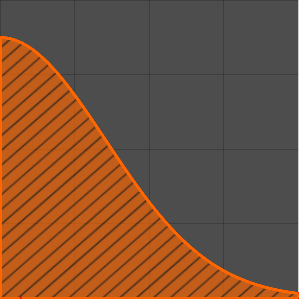
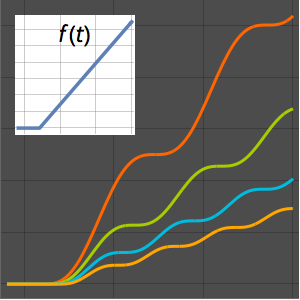
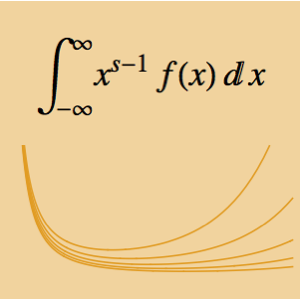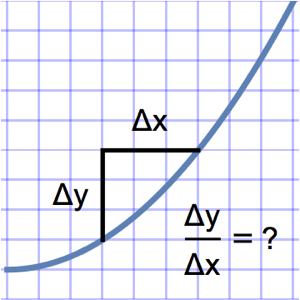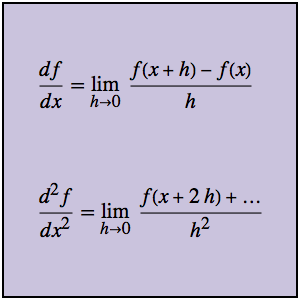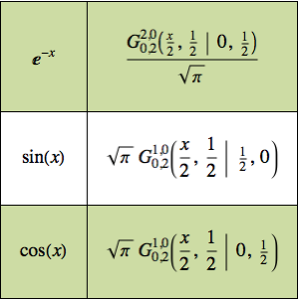Solución del problema de Tautócrona
El problema de tautócrona requiere encontrar la curva por donde el cordón colocado en cualquier parte caerá a la parte inferior en la misma cantidad de tiempo. Expresando el total de tiempo de caída en términos de la longitud de arco de la curva y la velocidad 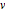 se obtiene la ecuación integral de Abel
se obtiene la ecuación integral de Abel 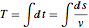 . Definiendo la función desconocida
. Definiendo la función desconocida 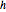 por la relación
por la relación 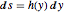 y usando la conservación de ecuación de energía
y usando la conservación de ecuación de energía 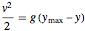 se obtiene la siguiente ecuación explícita.
se obtiene la siguiente ecuación explícita.
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Utilice DSolveValue para resolver la ecuación de integral.
dsdy = DSolveValue[abeleqn, h[y], y]Usando la relación 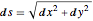 , resuelva
, resuelva 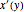 .
.
dxdy = Sqrt[dsdy^2 - 1]Comenzando la curva a partir del origen e integrando se obtiene 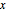 como una función de
como una función de 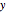 . Note que los supuestos aseguran que el integrando tenga un valor real.
. Note que los supuestos aseguran que el integrando tenga un valor real.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]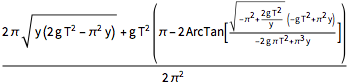
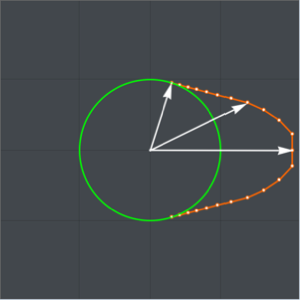
Usando un tiempo descendente de dos segundos y sustituyendo en el valor de la aceleración gravitacional, represente gráficamente la curva máxima para el tautócrona. (La rama 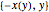 provine de la solución
provine de la solución 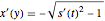 para la derivada de
para la derivada de 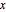 .)
.)
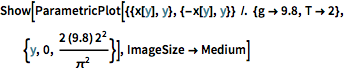
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]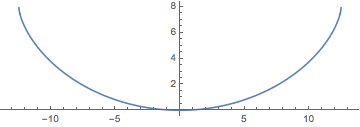
Cambiando las variables 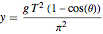 da una parametrización simple, no singular de la curva con
da una parametrización simple, no singular de la curva con 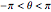 .
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Combinando la conservación de ecuación de energía y la regla de cadena 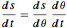 produce la siguiente ecuación diferencial para
produce la siguiente ecuación diferencial para 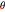 como una función de
como una función de 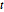 , la cual puede ser resuelta numéricamente.
, la cual puede ser resuelta numéricamente.
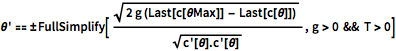
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]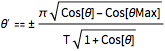
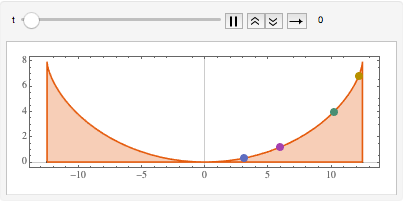
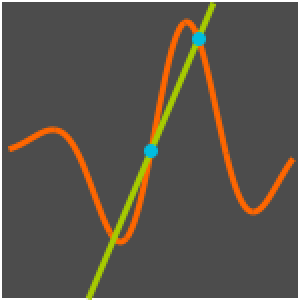
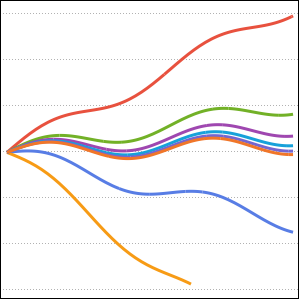
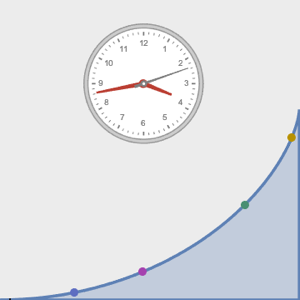
Visualice el movimiento a lo largo de la tautócrona.