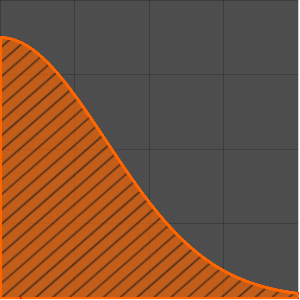
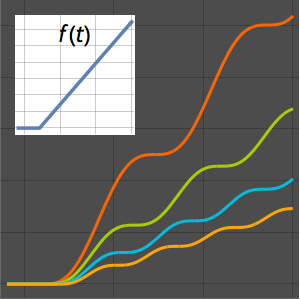
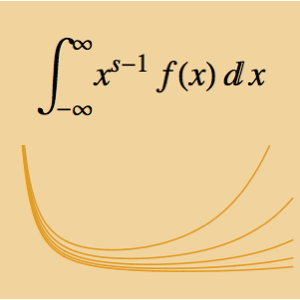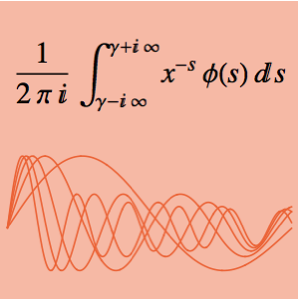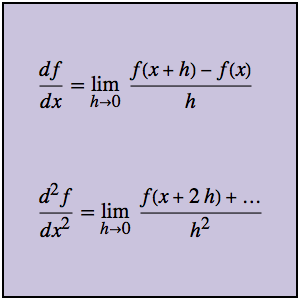解等时曲线问题: Wolfram语言 11 的新功能

解等时曲线问题

等时曲线问题是要找到一条曲线，使得位于曲线上任何位置的珠子滚到底部所用的时间都是相同的. 用弧长和速率 v 来表示滚落的时间，得到阿贝尔积分方程 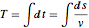. 由关系式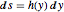来定义未知函数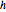，并利用能量守恒方程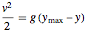得出下面的显式方程.

In[1]:=

abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\), 
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);

用 DSolveValue 解这个积分方程.

In[2]:=

dsdy = DSolveValue[abeleqn, h[y], y]

Out[2]=

应用公式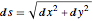求解 .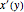

In[3]:=

dxdy = Sqrt[dsdy^2 - 1]

Out[3]=

让曲线从原点开始，并进行积分给出作为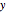的函数的 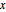. 注意其中的假设确保被积函数是实值的.

In[4]:=

x[y_] = Integrate[dxdy, {y, 0, y}, 
  Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]

Out[4]=

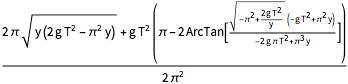
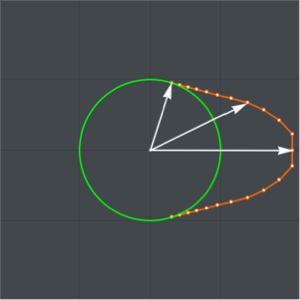
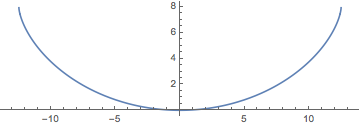
取两秒的滚落时间，并代入重力加速度，对最大的等时曲线作图. 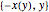（分支来自于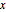的导数的解）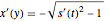

In[5]:=

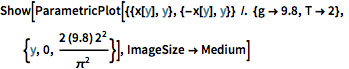
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
    0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]

Out[5]=

作变量替换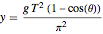，给出一个简洁的、非奇异的参数化曲线方程，其中 .

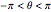In[6]:=

c[\[Theta]_] = (
   g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;

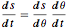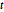结合能量守恒方程和复合函数求导法则（链式法则），给出作为的函数的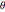的微分方程，而该方程可用数值方法求解.

In[7]:=

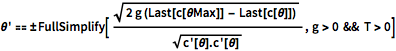
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
   2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
   c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]

Out[7]=

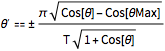
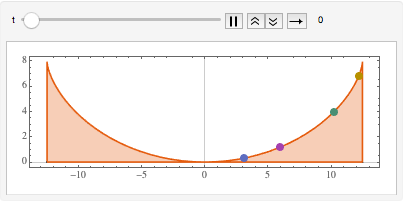
用图形演示沿等时曲线的运动.

播放动画

停止播放动画

Wolfram 语言™

解等时曲线问题

相关范例