Zipf의 법칙

지프의 법칙은 주어진 언어 자료에 있어서 어떤 단어의 빈도는 빈도 테이블에서 전반적인 단어 목록의 랭크에 반비례하는 법칙을 말합니다. 예를 들어, 새로운 함수의 WordCount와 WordCounts를 사용하여 Michael Cervantes의 소설 돈키호테 를 통해 지프의 법칙을 살펴봅니다.

ExampleData는 돈키호테 1권의 스페인어 텍스트를 포함하고 있습니다.

In[1]:=

textSpanish = ExampleData[{"Text", "DonQuixoteISpanish"}];

아래의 샘플은 18만개 이상의 단어가 포함되어 있습니다.

In[2]:=

WordCount[textSpanish]

Out[2]=

각각의 다른 단어의 수가 WordCounts에 의해 연상으로 주어집니다. 결과는 숫자의 내림차순으로 정렬됩니다.

The result is already sorted by decreasing counts.

In[3]:=

association = WordCounts[textSpanish];

In[4]:=

Take[association, 10]

Out[4]=

가장 많이 사용되는 1,000개 단어를 추출합니다.

In[5]:=

counts = Take[Values@association, 1000];

멱법칙을 사용하여 이러한 숫자를 근사하고, 선형 피팅의 사용을 위해 대수를 취합니다. 지프의 법칙에서 지수는 약 -1이어야한다고 주장하며, 이것에 가까운 값을 결과로 얻습니다.

In[6]:=

f[x_] = Fit[Log[Transpose[{Range[1000], counts}]], {1, x}, x]

Out[6]=

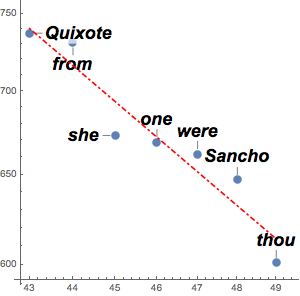
실제 데이터와 함께 피팅을 시각화합니다.

In[7]:=

Show[ ListLogLogPlot[counts, PlotStyle -> PointSize[0.02]], LogLogPlot[Exp[f[Log[x]]], {x, 1, 1000}, PlotStyle -> Directive[DotDashed, Red]], AspectRatio -> 1, PlotRange -> All ]

Out[7]=

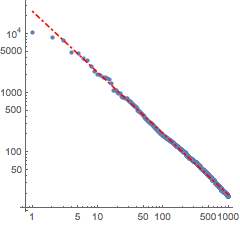
지프의 법칙은 모든 언어에서 적용되므로 영어 돈키호테에 대해서도 같은 계산이 실시됩니다.

In[8]:=

textEnglish = ExampleData[{"Text", "DonQuixoteIEnglish"}];

In[9]:=

associationEnglish = WordCounts[textEnglish]; countsEnglish = Take[Values@associationEnglish, 1000];

In[10]:=

Take[associationEnglish, 10]

Out[10]=

여기서도 역시 구해진 지수는 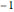에 가깝습니다.

In[11]:=

Fit[Log[Transpose[{Range[1000], countsEnglish}]], {1, x}, x]

Out[11]=