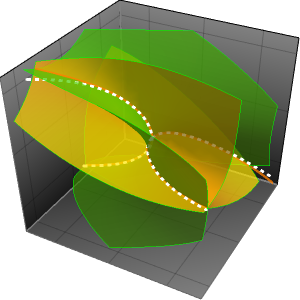
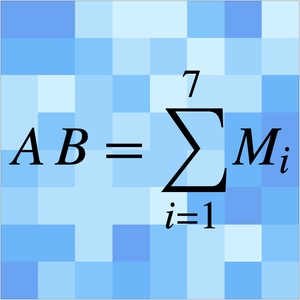Die Komplexität eines Problems ermitteln
Wenn man die Komplexitätsklasse eines Algorithmus bezeichnen möchte, gibt man immer die einfachste Funktion an, die AsymptoticEqual (großes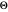 
) der exakten Laufzeitfunktion ist. Man kann dies auch so ausdrücken, dass jede Funktion sowohl AsymptoticLessEqual (großes 
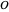) als auch AsymptoticGreaterEqual (großes 
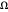) ist als die andere ist. Diese Konzepte veranschaulicht der Strassen-Algorithmus, der erste subkubische Algorithmus zur Matrizenmultiplikation.
Der Algorithmus besteht aus vier Schritten: jede der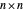 
Matrizen wird in 4 Teilmatrizen zerlegt, und bildet 14 lineare Kombinationen aus den 8 Teilmatrizen. Es werden 7 Ziffernpaare multipliziert und deren Ergebnisse summiert. Die Laufzeit 
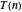besteht also aus konstanter Zeit 
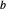für die Matrixzerlegung, 
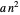für die Bildung linearer Kombinationen in Schritt 2 und 4 und 
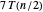für den dritten Schritt.
Lösen Sie die Rekursionsgleichung:
Obwohl das Ergebnis kompliziert ist, gilt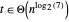 
.
Dementsprechend gilt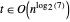 
und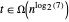 
.
Beachten Sie, dass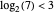 
, der Algoritmus ist daher subkubisch.
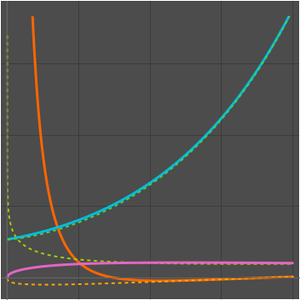
Vergleichen Sie die Wachstumsrate der Rechenzeit des naiven kubischen Algorithmus und des Strassen-Algorithmus.
