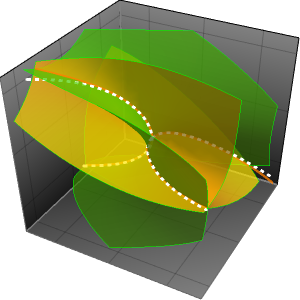
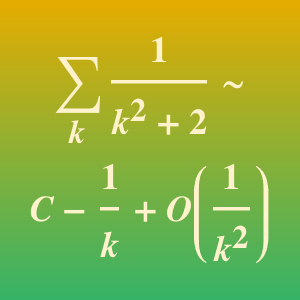Asymptotische Näherungen überprüfen
Wenn sich eine Funktion 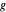 mit einem relativen Fehler einer Funktion
mit einem relativen Fehler einer Funktion 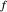 nähert, die verschwindet, wenn sie sich dem Ursprunkt nährert, dann gilt
nähert, die verschwindet, wenn sie sich dem Ursprunkt nährert, dann gilt 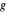 als AsymptoticEquivalent zu
als AsymptoticEquivalent zu 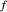 , was häufig als
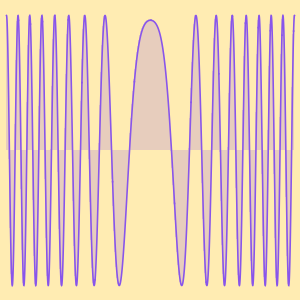
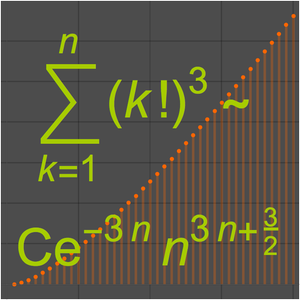
, was häufig als 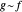 geschrieben wird. Ein klassisches Beispiel ist die Stirlingformel, mit der man für große Fakultäten Näherungswerte berechnen kann.
geschrieben wird. Ein klassisches Beispiel ist die Stirlingformel, mit der man für große Fakultäten Näherungswerte berechnen kann.
Da der relative Fehler gegen Null geht, tendiert das Verhältnis der Funktionen gegen 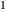 .
.
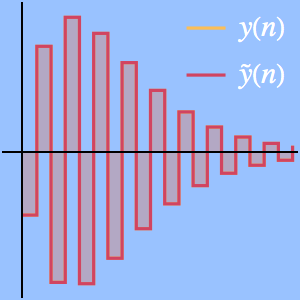
Stirlings Näherungsformel verblüfft, weil der absolute Fehler gegen unendlich geht, während der relative Fehler gegen Null geht.
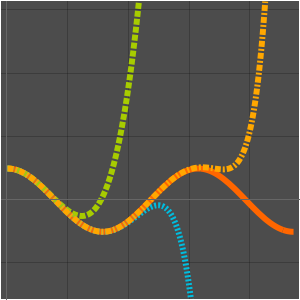
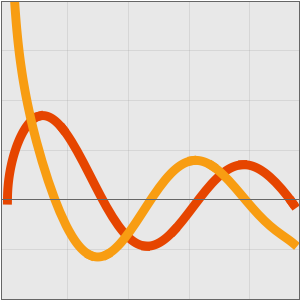
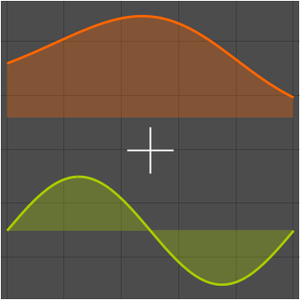
Die Taylor-Reihe liefert asymptotische Näherungen.
Mit einer Laurent-Reihe können auch asymptotische Näherungen gemacht werden.
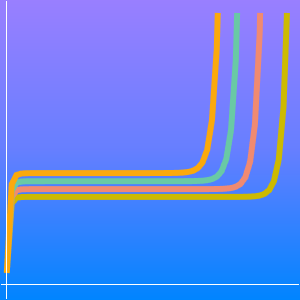
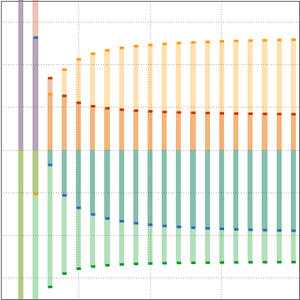
Der Primzahlsatz besagt, dass 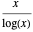 eine asymptotische Näherung der Primzahlzählfunktion
eine asymptotische Näherung der Primzahlzählfunktion 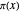 ist.
ist.
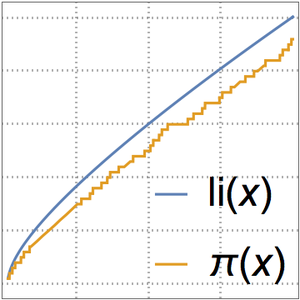
Eine bessere Approximation wird durch die logarithmische Integralfunktion 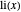 erreicht.
erreicht.
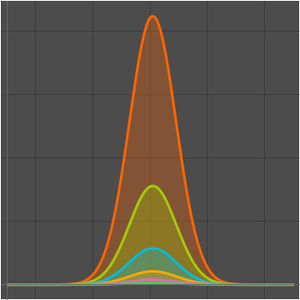
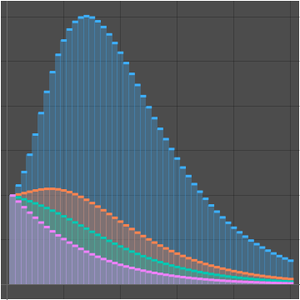
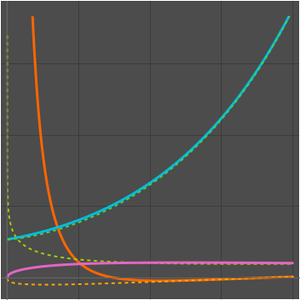
Vergleichen Sie die Primzahlzählfunktion und die beiden Näherungswerte.