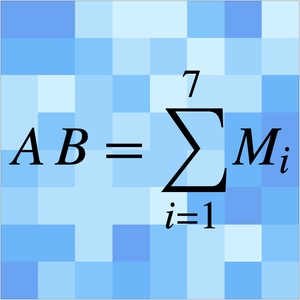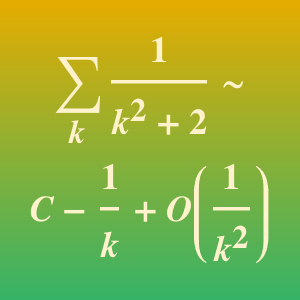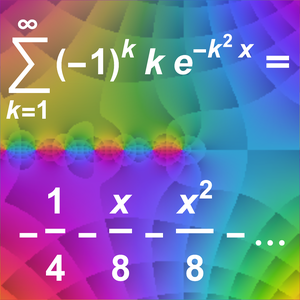Eine Taylor-Entwicklung für eine exponentielle Summe (AsymptoticSum)
Asymptotische Methoden können nützliche Näherungswerte für unendliche Summen liefern, die von einem Parameter abhängen. Dieses Beispiel zeigt, wie eine unendliche Exponentialsumme mit einer Taylor-Entwicklung in Bezug auf den Parameter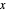 
im Summanden approximiert werden kann. Die Koeffizienten der Taylor-Reihe werden durch Berechnen der Reste an den Polen der Mellin-Transformation für diese Summe erhalten.
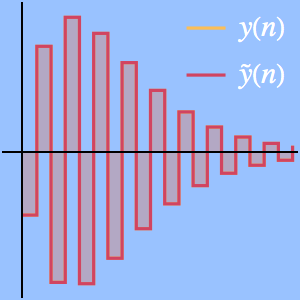
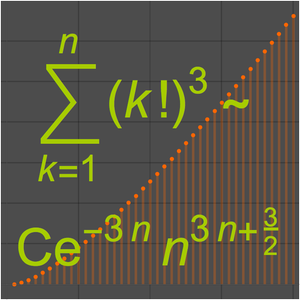
Ermitteln Sie eine Taylor-Approximation für eine alternierende Gaußsche Exponentialsumme.
Vergleichen Sie dies mit einer numerischen Näherung.
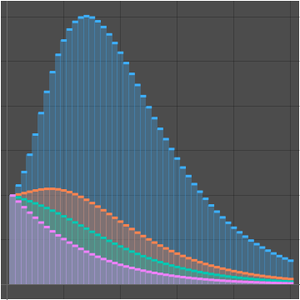
Die asymptotische Approximation basiert auf einer Mellin-Transformationsberechnung.
Die Koeffizienten der Taylor-Reihe werden aus den Polen der Summe berechnet.
