Visualisez les valeurs propres des graphes
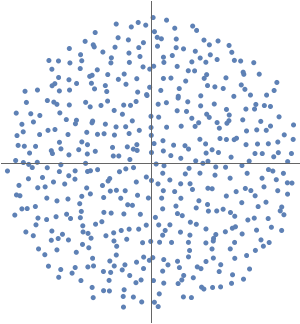
Les valeurs propres des graphes peuvent fournir des informations sur les propriétés structurelles du graphe.
Générez un graphe orienté acyclique à partir d'un graphe de base initial.
Si un graphe est acyclique, alors sa matrice d'adjacence est nilpotente et toutes ses valeurs propres sont nulles.
Si un graphe est symétrique, alors sa matrice d'adjacence est symétrique et ses valeurs propres sont réelles.
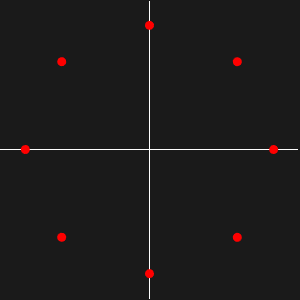
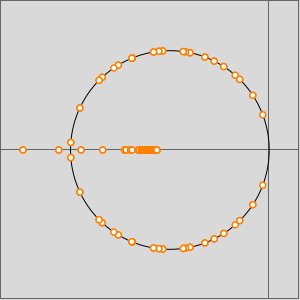
Si un graphe est biparti, alors le spectre de sa matrice d'adjacence est symétrique en rotation par rapport à 0. C'est-à-dire que si 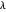 correspond à une valeur propre de la matrice d'adjacence, il en va de même pour
correspond à une valeur propre de la matrice d'adjacence, il en va de même pour 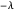 .
.
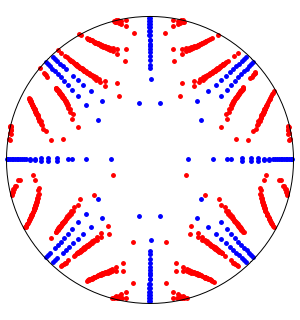
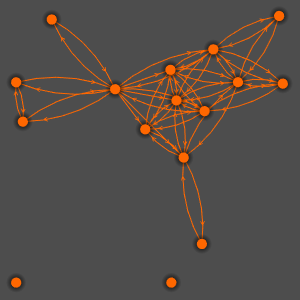
Générez un graphe montrant un ensemble de symboles liés les uns aux autres dans la documentation Wolfram.
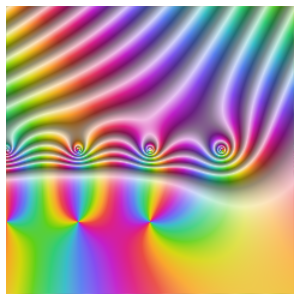
La représentation des valeurs propres du graphe montre que des cycles sont présents, mais que le graphe n'est ni symétrique ni biparti.
Le graphe n'est pas symétrique parce que ComplexExpand est lié à Complex, Conjugate, Im et Re, mais pas l'inverse.