Visualisez les singularités essentielles
Utilisez des outils de représentation graphique complexes pour visualiser les singularités essentielles de différentes manières.
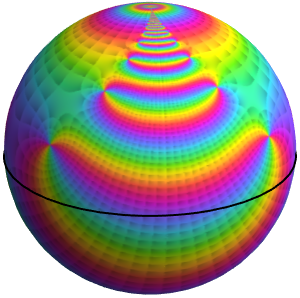
Définissez une fonction avec une singularité essentielle.
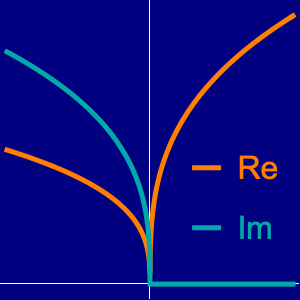
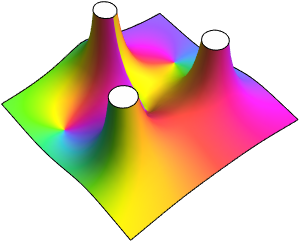
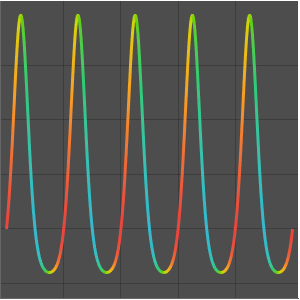
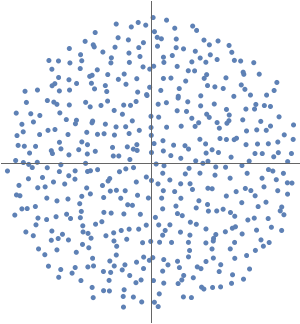
En tant que fonction d'une variable réelle, 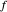 oscille infiniment et rapidement au voisinage de
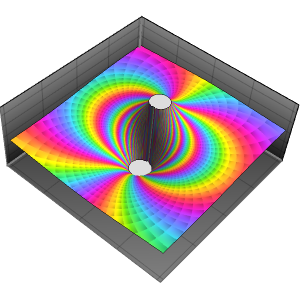
oscille infiniment et rapidement au voisinage de 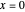 . À partir de ReImPlot, vous pouvez constater que la partie réelle et la partie imaginaire se comportent de la même façon lorsqu'elles sont proches de l'origine.
. À partir de ReImPlot, vous pouvez constater que la partie réelle et la partie imaginaire se comportent de la même façon lorsqu'elles sont proches de l'origine.
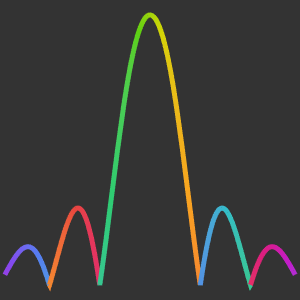
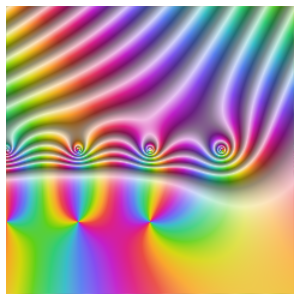
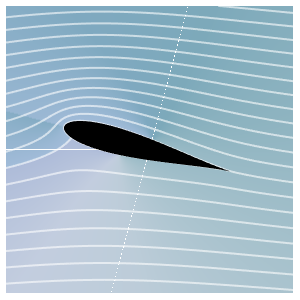
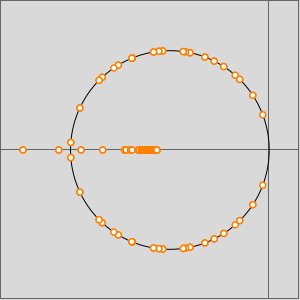
Les oscillations sont également représentées par AbsArgPlot. AbsArgPlot montre également que la valeur absolue se rapproche de zéro à taux constants des deux côtés.
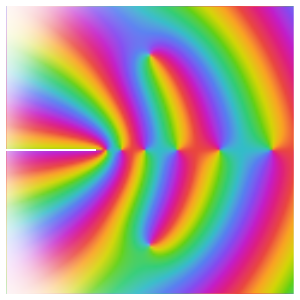
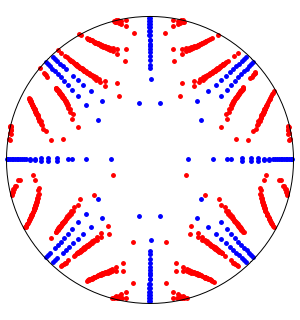
En se basant sur le comportement le long de l'axe réel, on pourrait supposer que la fonction converge vers zéro à l'origine. En examinant le comportement par rapport aux nombres complexes, on voit que ce n'est pas le cas, puisque la fonction y a une singularité essentielle.