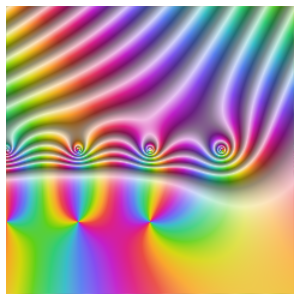
Valeurs propres d'une équation d'onde structurellement amortie
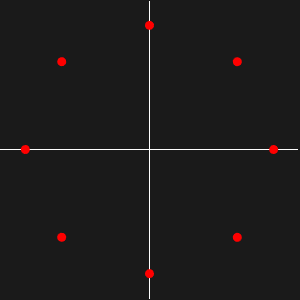
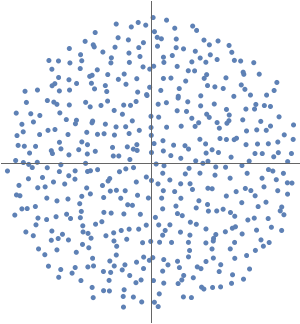
Analysez la stabilité des solutions d'une équation différentielle partielle en examinant ses valeurs propres. Toutes les valeurs propres d'un système stable comportent des parties réelles négatives.
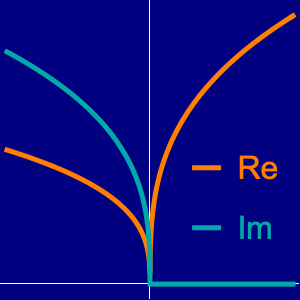
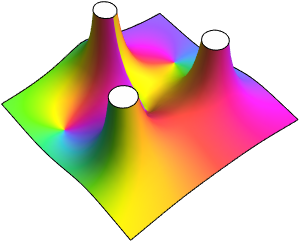
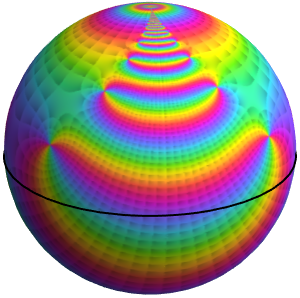
Calculez les 100 premières valeurs de 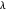 et
et 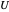 de telle sorte que
de telle sorte que 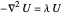 sur le disque unitaire et que
sur le disque unitaire et que 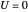 sur le cercle unitaire.
sur le cercle unitaire.
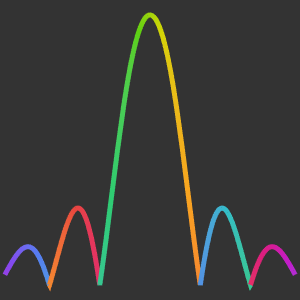
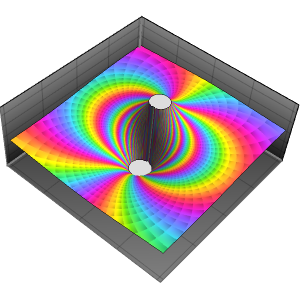
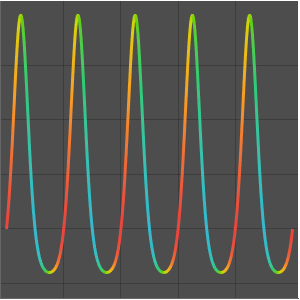
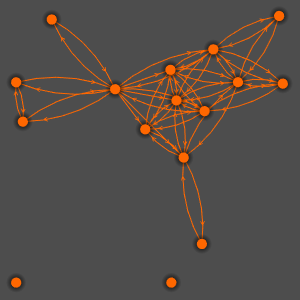
Utilisez les solutions précédentes pour résoudre l'équation d'onde structurellement amortie 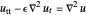 pour
pour 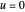 sur le disque unitaire en cherchant des solutions de la forme
sur le disque unitaire en cherchant des solutions de la forme  . Les valeurs plus petites de
. Les valeurs plus petites de 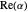 correspondent à des solutions qui se décomposent plus rapidement.
correspondent à des solutions qui se décomposent plus rapidement.
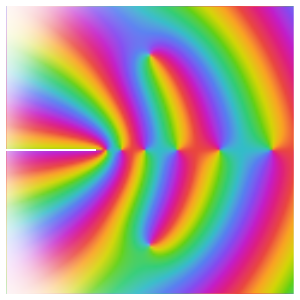
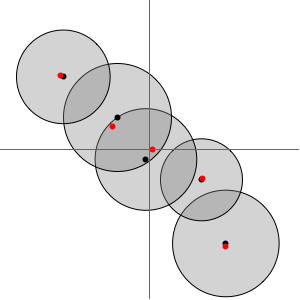
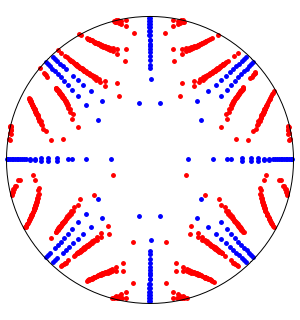
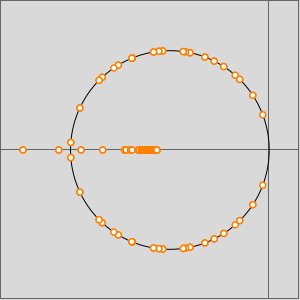
Visualisez l'effet du paramètre d'amortissement 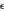 sur
sur 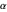 . Les valeurs de
. Les valeurs de 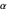 s'accumulent en
s'accumulent en 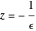 , et si
, et si 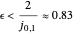 , alors il y a des valeurs propres non réelles sur le cercle de rayon
, alors il y a des valeurs propres non réelles sur le cercle de rayon 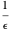 centré en
centré en 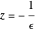 .
.