Les disques de Gerschgorin
Le théorème des cercles de Gerschgorin (http://mathworld.wolfram.com/GershgorinCircleTheorem.html) stipule que chaque valeur propre de la matrice carrée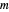 
se trouve dans au moins un des disques dont les centres correspondent aux entrées diagonales de 
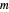et dont les rayons correspondent à une somme des entrées de chaque rang.
Générez une matrice complexe aléatoire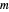 
.
Les entrées diagonales de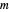 
correspondent aux centres des disques de Gerschgorin.
Le rayon du disque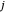 
ème de Gerschgorin, 
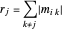, correspond à la somme des modules des entrées de la rangée 
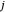, à l'exception de l'entrée diagonale.
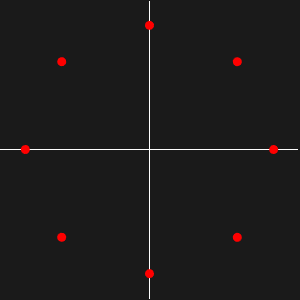
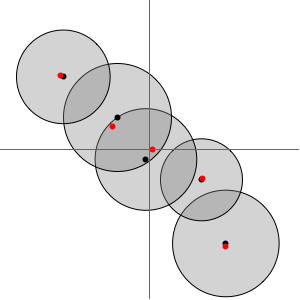
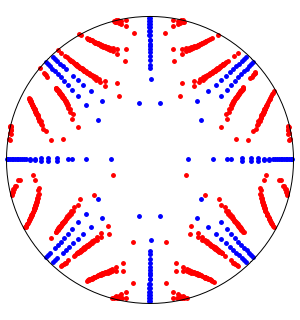
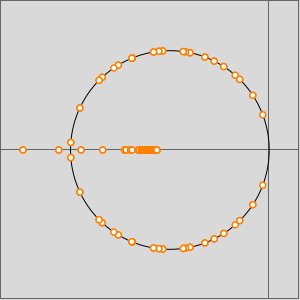
Créez les disques de Gerschgorin pour la matrice.
Affichez les valeurs propres (en rouge) dans les disques de Gerschgorin.
