Basis Pursuit
Bei einer Reihe von Basisfunktionen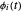 
kann ein Signal 
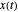durch die Linearkombination 
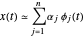approximiert werden. Je größer die Basis, desto besser kann ein Signal approximiert werden. Allerdings benötigen nicht alle Signale alle Basisfunktionen für eine sinnvolle Annäherung. Die Idee des Optimierungsproblems Basis Pursuit besteht darin, eine kleine Teilmenge einer größeren Menge von Basisfunktionen zu wählen, die überdeterminiert sein können.
Dieses Beispiel zeigt, wie die Basis Pursuit mit Fit und der Option FitRegularization einfach und effizient durchgeführt werden kann.
Für Signale mit diskreter Zeitabtastung kann die Rekonstruktion einfach als Matrixgleichung 
angegeben, wobei 
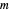die Matrix mit den Elementen 
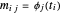ist. Für überdeterminierte Basen können die Koeffizienten α, die die beste Approximation liefern, einfach durch die Methode der kleinsten Quadrate gefunden werden. Wenn anstatt der Minimierung von 
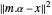eine L1-Regularisierung hinzugefügt wird, um 
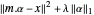zu ergeben, sind Komponenten von α null, wenn die Werte des Parameters 
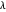groß genug sind. Das Problem kann mit Fit und der neuen Option FitRegularization effizient gelöst werden.
Verwenden Sie eine Basis von Gabor-Funktionen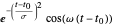 
und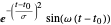 
in einem Beispiel mit einer umfangreichen Menge Basisfunktionen.
Hier ist ein Diagramm, das eine Auswahl von Gabor-Funktionen zeigt.
Im Intervall von 0 bis 1 mit einem Zeitabtastintervall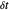 
, ist eine Reihe von Basisfunktionen mit 
, 
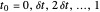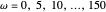und einem festgelegten 
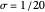ausreichend, um eine große Bandbreite an Signalen exakt darzustellen.
Die Basismatrix kann mit DesignMatrix erstellt werden.
Diese Matrix ist sehr groß, aber mit einem kleinen Verlust an Darstellungsgenauigkeit ist es möglich, die Tatsache zu nutzen, dass die Gabor-Funktionen durch die Verwendung eines Schwellenwerts schnell von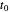 
zerfallen.
Sehen Sie sich nun ein Signal an.
Das Signal kann durch einfaches Auswerten aller Zeitabtastungen diskretisiert werden.
Eine Anpassung mit der Methode der kleinsten Quadrate gibt an, wie gut die Funktion durch die Basisfunktionen dargestellt werden kann. Das dauert lange, weil die Matrix so groß ist.
Der vollständige Darstellungsfehler ist praktisch die maschinengenaue Rundung.
Verwenden Sie nun die L1-Regularisierung, um einen Sparse Fit zu finden. Dies ist als Anpassung mit der Methode der kleinsten Quadrate tatsächlich schneller zu berechnen, da die Regularisierung einen dünn besetzten Algorithmus verwendet.
Die dünn besetzte Abbildung verwendet nur 50 von 30561 Basiselementen. Diese ist klein genug, um tatsächlich eine funktionale Form zu erhalten.
Show the error.
Die Anpassung kann leicht verbessert werden, indem man mit genau diesen Basiselementen die Methode der kleinsten Quadrate verwendet.
Der Fehler kann durch Ändern des Parameters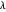 
behoben werden. Im Allgemeinen führt ein größeres 
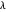zu weniger Basisfunktionen und mehr Fehlern, während ein kleineres 
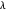zu mehr Basisfunktionen und weniger Fehlern führt. Hier sind Fehlerdiagramme für andere Werte von 
.
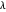