Decomposição em modos
Dado um conjunto de funções básicas 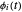 , um sinal
, um sinal 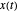 pode ser aproximado pela combinação linear
pode ser aproximado pela combinação linear 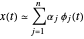 . Normalmente, quanto maior a base, melhor o sinal pode ser aproximado. No entanto, nem todos os sinais precisam de todas as funções básicas para uma aproximação razoável. A idéia de decomposição em modos é escolher um pequeno subconjunto de um conjunto maior, ou dicionário, de funções básicas que podem ser sobredeterminadas.
. Normalmente, quanto maior a base, melhor o sinal pode ser aproximado. No entanto, nem todos os sinais precisam de todas as funções básicas para uma aproximação razoável. A idéia de decomposição em modos é escolher um pequeno subconjunto de um conjunto maior, ou dicionário, de funções básicas que podem ser sobredeterminadas.
Este exemplo demonstra como a decomposição em modos pode ser feita de maneira fácil e eficiente usando Fit com a opção FitRegularization.
Para sinais com amostragem de tempo discreto, a reconstrução pode ser simplesmente dada como uma equação matricial 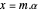 , onde
, onde 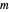 é a matriz com elementos
é a matriz com elementos 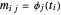 . Para bases sobredeterminadas, os coeficientes α que dão a melhor aproximação podem simplesmente ser encontrados por mínimos quadrados. Se, em vez de minimizar
. Para bases sobredeterminadas, os coeficientes α que dão a melhor aproximação podem simplesmente ser encontrados por mínimos quadrados. Se, em vez de minimizar 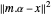 , um termo de regularização L1 é adicionado para dar
, um termo de regularização L1 é adicionado para dar 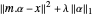 , valores suficientemente grandes do parâmetro
, valores suficientemente grandes do parâmetro 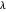 incentivam componentes de α a serem zero. O problema pode ser resolvido com eficiência usando Fit com a nova opção FitRegularization.
incentivam componentes de α a serem zero. O problema pode ser resolvido com eficiência usando Fit com a nova opção FitRegularization.
Use uma base de funções Gabor 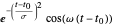 e
e 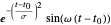 para um exemplo de um grande dicionário de funções básicas.
para um exemplo de um grande dicionário de funções básicas.
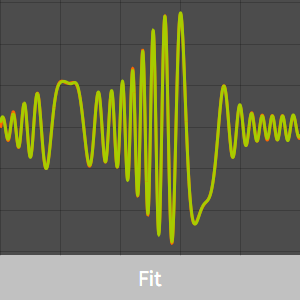
Aqui está um gráfico mostrando uma amostra das funções do Gabor.
No intervalo de 0 a 1 com um intervalo de amostragem de tempo 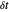 , um conjunto de funções básicas com
, um conjunto de funções básicas com 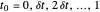 ,
, 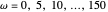 e
e 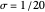 fixado, são suficientes para representar exatamente uma ampla variedade de sinais.
fixado, são suficientes para representar exatamente uma ampla variedade de sinais.
A matriz de base pode ser construída usando DesignMatrix.
Esta matriz é muito grande, mas com uma pequena perda na precisão da representação, é possível usar o fato de que as funções de Gabor decaem rapidamente de 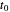 para torná-la esparsa, usando um limite.
para torná-la esparsa, usando um limite.
Agora considere um sinal.
O sinal pode ser discretizado simplesmente calculando todas as amostras de tempo.
Um ajuste de mínimos quadrados indicará quão bem a função pode ser representada pelas funções de base. Isso leva muito tempo porque a matriz é muito grande.
O erro de representação completo é efetivamente arredondamento de precisão da máquina.
Agora use a regularização L1 para encontrar um ajuste esparso. Na verdade, isso é mais rápido de calcular do que o ajuste de mínimos quadrados, pois ele usa um algoritmo esparso.
A representação esparsa usa apenas 50 dos 30561 elementos de base. Isso é pequeno o suficiente para realmente ter uma forma funcional.
Mostre o erro.
O ajuste pode ser melhorado ligeiramente fazendo um ajuste de mínimos quadrados apenas com esses elementos de base.
O erro pode ser ajustado alterando o parâmetro 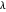 . Geralmente,
. Geralmente, 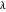 maiores resultarão em menos funções básicas e mais erros, enquanto
maiores resultarão em menos funções básicas e mais erros, enquanto 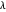 menores resultarão em mais funções de base e menor erro. Aqui estão os gráficos de erros para outras opções de
menores resultarão em mais funções de base e menor erro. Aqui estão os gráficos de erros para outras opções de 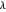 .
.