Búsqueda de bases
Dado un conjunto de funciones básicas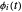 
, una señal 
puede ser aproximada por la combinación lineal 
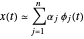. Típicamente, mientras más grande sea la base, mejor será la aproximación de la señal. Sin embargo, no todas las señales necesitan todas las funciones base para una aproximación razonable. La idea de la búsqueda de bases es elegir un pequeño subconjunto de un conjunto más grande o diccionario de funciones básicas que puedan estar sobredeterminadas.
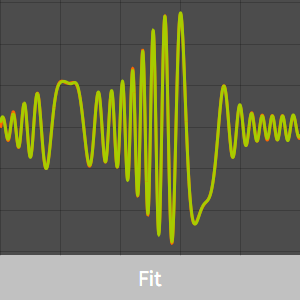
Este ejemplo demuestra cómo la búsqueda de bases puede ser realizada de manera fácil y eficiente utilizando Fit con la opción FitRegularization.
Para señales con muestreo de tiempo discreto, la reconstrucción puede ser simplemente dada como una ecuación de matriz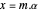 
, donde 
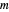es la matriz con elementos 
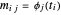. Para bases sobredeterminadas, los coeficientes α que dan la mejor aproximación pueden ser encontrados fácilmente por medio de mínimos cuadrados. Si, en lugar de minimizar 
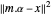, se agrega un término de regularización L1 para dar 
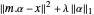, los valores suficientemente grandes del parámetro 
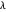estimulan a los componentes de α a que sean cero. El problema puede ser resuelto de forma eficiente usando Fit con la nueva opción FitRegularization.
Use una base de funciones de Gabor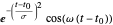 
y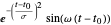 
para un ejemplo de un extenso diccionario de funciones base.
Aquí tenemos un gráfico presentando una muestra de funciones de Gabor.
En el intervalo de 0 a 1 con un intervalo de tiempo de muestra 
, un conjunto de funciones básicas con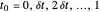 
, 
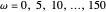y un 
fijo son suficientes para representar exactamente una amplia variedad de señales.
La matriz base puede ser construida usando DesignMatrix.
Esta matriz es muy grande, pero con una pequeña pérdida en la precisión de la representación es posible utilizar el hecho que las funciones de Gabor se descomponen rápidamente desde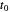 
para que sea escaso utilizando un umbral.
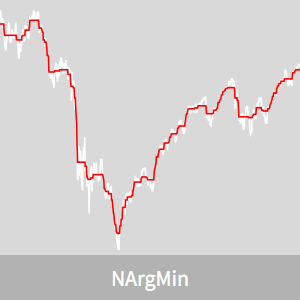
Ahora considere una señal.
La señal puede ser discretizada con tan solo evaluar en todas las muestras de tiempo.
Un ajuste de mínimos cuadrados indicará qué tan bien puede ser representada la función por las funciones básicas. Esto toma mucho tiempo porque la matriz es muy extensa.
El error de representación completa es efectivamente el redondeo de precisión de máquina.
Ahora use la regularización L1 para encontrar un ajuste disperso. En realidad, esto es más rápido de calcular que el ajuste de mínimos cuadrados, ya que utiliza un algoritmo disperso.
La representación dispersa utiliza solo 50 de los 30561 elementos básicos. Esto es lo suficientemente pequeño como para obtener una forma funcional.
Muestre el error.
El ajuste se puede mejorar ligeramente haciendo un ajuste de mínimos cuadrados con solo esos elementos básicos.
El error se puede ajustar cambiando el parámetro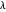 
. Generalmente, un 
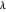más grande resultará en menos funciones básicas y más errores, mientras que un 
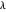más pequeño resultará en más funciones básicas y menos errores. Aquí tenemos gráficos de error para las otras opciones de 
.
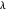