基底追跡
基底関数 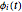 の集合が与えられたとき,信号
の集合が与えられたとき,信号 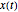 は線形結合
は線形結合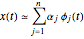 によって近似することができる.通常,基底が大きければ大きいほど,信号の近似は向上する.しかし妥当な近似のために,すべての信号がすべての基底関数を必要としているわけではない.基底追跡とは,過剰決定される可能性のある基底関数の大きい集合(辞書)の小さい部分集合を選ぶことである.
によって近似することができる.通常,基底が大きければ大きいほど,信号の近似は向上する.しかし妥当な近似のために,すべての信号がすべての基底関数を必要としているわけではない.基底追跡とは,過剰決定される可能性のある基底関数の大きい集合(辞書)の小さい部分集合を選ぶことである.
この例では,FitのFitRegularizationオプションを使って簡単かつ効率的に基底追跡を行う方法を示す.
離散時間サンプリングの信号では,再構成は行列方程式 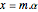 として与えることができる.ここで
として与えることができる.ここで 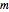 は要素
は要素 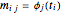 を持つ行列である.過剰決定系の基底関数では,最高の近似を与える係数 α は最小二乗により簡単に見付けられる.
を持つ行列である.過剰決定系の基底関数では,最高の近似を与える係数 α は最小二乗により簡単に見付けられる.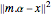 を最小化する代りに,
を最小化する代りに,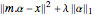 を与えるためにL1正規化項が加えられると,パラメータ
を与えるためにL1正規化項が加えられると,パラメータ 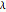 に対して十分大きい値により,α はゼロになろうとする.Fitで新しいオプションFitRegularizationを使うと,問題を効率的に解くことができる.
に対して十分大きい値により,α はゼロになろうとする.Fitで新しいオプションFitRegularizationを使うと,問題を効率的に解くことができる.
基底関数の大きい辞書の例としてガボール(Gabor)関数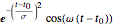 および
および 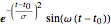 の基底を使う.
の基底を使う.
ガボール関数のサンプルを示すプロットである.
時間サンプル間隔 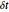 の0から1の区間において,
の0から1の区間において,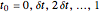 ,
,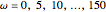 ,固定された
,固定された 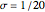 の基底関数の集合は,多様な信号を厳密に表すのに十分である.
の基底関数の集合は,多様な信号を厳密に表すのに十分である.
基底行列はDesignMatrixを使って構築することができる.
この行列は非常に大きいが,表現の確度をわずかに失うだけで,ガボール関数が 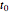 から急速に減衰して,閾値を使って疎になるというという特性を使うことができる.
から急速に減衰して,閾値を使って疎になるというという特性を使うことができる.
信号を考える.
この信号は,すべての時間サンプルで評価するだけで離散化することができる.
最小二乗フィットによって,この関数が基底関数でいかによく表現されているかが分かる.行列が非常に大きいので,これには時間がかかる.
全体の表現誤差は,実質的に機械精度の丸めによる.
L1正規化を使って,疎なフィットを求める.この方法は疎なアルゴリズムを使うため,最小二乗フィットよりも速く計算できる.
疎表現には30561個の基底成分のうちの50個しか使われていない.これだけ小さいと,関数形式が得られる.
誤差を示す.
これらの基底成分だけで最小二乗フィットを行うことで,フィットはわずかに向上する.
パラメータ 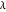 を変更することで誤差を調整することができる.一般に
を変更することで誤差を調整することができる.一般に 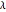 が大きいと基底関数の数は少なく誤差が多くなる.一方,
が大きいと基底関数の数は少なく誤差が多くなる.一方, 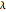 が小さいと基底関数の数は多く,誤差は小さくなる。
が小さいと基底関数の数は多く,誤差は小さくなる。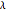 を変更したときの誤差プロットである.
を変更したときの誤差プロットである.