体积最大的长方体
求内接在凸多面体中的体积最大的轴平行立方体 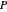 。
。
这个例子演示了如何用 power-cone 约束条件来表示正的项的乘积的优化,可将约束条件与 ConicOptimization 一起使用以找到最优解。
考虑一个以随机点的凸包形式构建的随机凸多面体 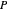 。
。
对于长方体,找到一个下边角点 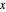 和边长向量
和边长向量 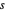 ,从而可用 Wolfram 语言
,从而可用 Wolfram 语言 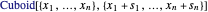 来表示该长方体。长方体的体积为边长的乘积所以目标函数就是最大化
来表示该长方体。长方体的体积为边长的乘积所以目标函数就是最大化 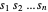 。如果长方体的所有边角都在
。如果长方体的所有边角都在 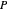 中,那么长方体中的所有点也是如此。可用
中,那么长方体中的所有点也是如此。可用 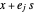 来描述边角,其中
来描述边角,其中 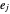 位于
位于 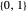 中所有可能的 n‐tuples 元素的集合
中所有可能的 n‐tuples 元素的集合 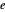 中。
中。
问题变为:
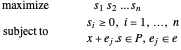
因为 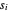 非负,最大化乘积
非负,最大化乘积 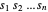 与最大化几何平均
与最大化几何平均 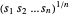 (已知是凹的)是一样的。最大化
(已知是凹的)是一样的。最大化 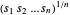 等价于最小化
等价于最小化 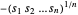 (是凸的)。通过辅助变量
(是凸的)。通过辅助变量 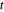 将问题重新用线性目标函数 -
将问题重新用线性目标函数 -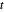 表示,约束条件为
表示,约束条件为 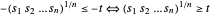 。
。
问题变为:
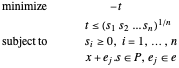
power cone 是 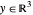 的集合,满足
的集合,满足 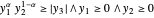 ,可用 Wolfram 语言
,可用 Wolfram 语言 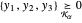 表示。
表示。
因为 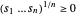 ,对于非负的
,对于非负的 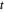 ,可满足新的约束条件
,可满足新的约束条件 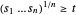 ,且等价于
,且等价于 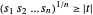 。可写作以下 power cone 约束条件:
。可写作以下 power cone 约束条件:
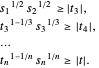
如果 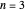 ,问题变为:
,问题变为:
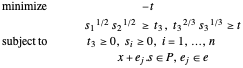
凸多面体可以表示为半空间 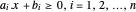 的交叉点。提取每个边的系数
的交叉点。提取每个边的系数 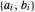 。
。
求解问题。
显示体积最大的内接长方体。
除了多面体,取任何可用凸锥表示的集合 K⊆n,如一个椭球。当且仅当 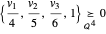 时,长方体的顶点
时,长方体的顶点 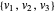 才位于椭球中。
才位于椭球中。
求解问题。
绘制结果。