稳健的数据拟合
通过最小化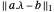 
给出非线性离散数据的稳健拟合。
下面的例子演示了如何使用矩阵、向量变量和向量不等式将拟合问题轻松转换为优化问题。
生成含有异常值的噪声数据。
用基函数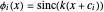 
拟合数据。近似模型为 
。
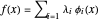可使用函数 DesignMatrix 获取设计矩阵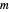 
，其中的元素为 
。
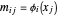响应是每个数据点的第二个元素。
通过引入向量变量 s 最小化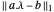
，使得 s 的每个分量满足 
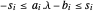，以便 
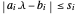。可用 VectorLessEqual 一次性表示所有分量的条件。
范数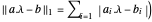 
是凸的，条件 
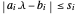也是凸的，最小化
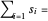Total[s] 相当于最小化范数 
。
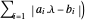可用有明确数值的方程来定义参数值。这里，参数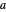 
和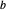 
是根据设计矩阵和响应来定义的。
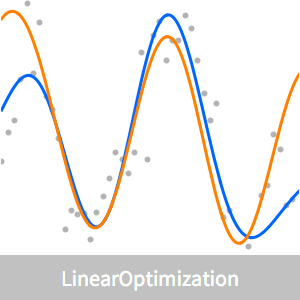
可视化拟合。
将近似模型与最小二乘拟合进行比较。
注意，这两种拟合都可以直接用 Fit 完成。用以下步骤完成 L1 拟合。
最小二乘拟合是 Fit 的默认值，用以下步骤完成。
