解析中心
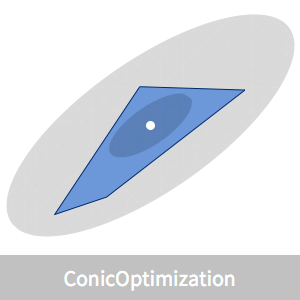
凸多边形可以表示为半平面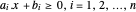 
的交叉点。解析中心被定义为多边形内部的一个点，它可以最大化到各个边的距离的乘积。多边形内一个点 
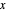到各个边的距离为 
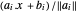，所以解析中心是最大化 
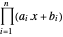的点 
。
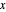这个例子演示怎样以不同方式将指数锥约束条件与 ConicOptimization 一起使用来求解析中心，以及怎样用 LinearOptimization 提取多边形的不等式表示。
取一个凸多边形。
提取每个边的系数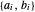 
。
对应于多边形的标量不等式为：
为了将问题表示为凸最小化问题，取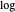 
并将目标函数 
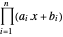取负。转换后的目标函数为 
。
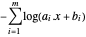因为对数之和是凹的，取负后就变成凸的，所以可引入辅助变量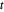 
c作为目标函数，
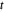受约束条件 
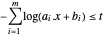的限制。
可视化解析中心的位置。
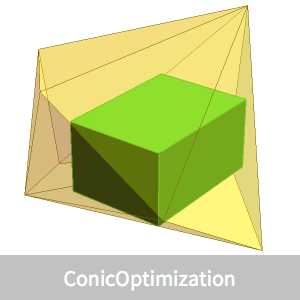
有一些简单的公式可以给出以解析中心为中心的内切和外覆椭圆。
