寻找基函数
给定一组基函数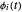 
，可通过线性组合 
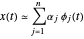来近似信号 
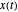。通常，基函数越多，对信号的近似越好。然而，不是所有信号都需要使用全部基函数才能进行合理的近似。寻找基函数的要点是从过定的较大的基函数集合中选择小子集。
这个例子演示了如何使用带有 FitRegularization 选项的 Fit 轻松有效地完成寻找基函数的任务。
对于离散时间采样信号，可用矩阵方程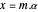 
进行重建，其中 
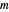是元素为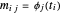 
的矩阵。对于过定的基函数，可通过最小二乘法求得给出最佳近似的系数 α。如果不是最小化 
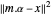，则添加 L1 正则化项，从而得出 
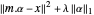，如果参数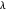 
足够大，则希望 α 中的分量为零。可通过使用带有新选项 FitRegularization 的 Fit 有效解决问题 。
使用 Gabor 函数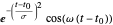 
和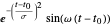 
作为基函数。
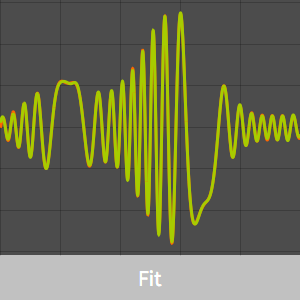
下面的图显示了 Gabor 函数的一个样本。
在从 0 到 1 的区间内，时间抽样间隔为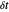 
，由 
、
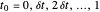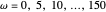及恒定的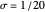 
所确定的一组基函数足以准确地表示各种各样的信号。
可用 DesignMatrix 构建基矩阵。
矩阵非常大，但表示精度 (representation accuracy) 损失很小，可以通过使用 Gabor 函数从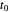 
处快速衰减的事实，利用一个阈值使其变成稀疏矩阵。
现在来看一个信号。
只需在所有时间样点上进行计算即可对信号进行离散化。
最小二乘拟合将表明用基函数表示函数的好坏程度。这需要很长时间，因为矩阵太大了。
全部的表示误差实际上是机器精度舍入带来的。
现在用 L1 正则化求稀疏拟合。实际上计算速度比最小二乘拟合更快，因为它使用稀疏算法。
稀疏表示仅使用了 30561 个基函数中的50 个。这已足以形成函数的形式。
显示误差。
通过仅用那些基本元素进行最小二乘拟合，可以略微改善拟合。
可以通过更改参数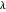 
来调整误差。通常，较大的 
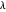将导致更少的基函数和更大的误差，较小的 
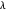将导致更多的基函数和更小的误差。下面是 
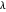取其他值时的误差图。
