最佳平面规划

来考虑以下问题：将 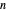个小长方形置于周长最小的较大的长方形内，对相对位置、长宽比、较小矩形之间的间距和面积进行限制。

这个例子演示如何使用 Wolfram 语言定义一个函数，该函数将通过 NMinimize 来解决平面规划问题。该函数将使用向量不等式，包括半定不等式。

用 Rectangle[{0, 0}, {H, W}] 描述较大的长方形，用 r_i=Rectangle[{x_i, y_i}, {x_i+w_i, y_i+h_i}], i=1 … n 描述较小的长方形。

可用两个有向图来描述相对位置，一个用来描述水平放置，另一个用来描述垂直放置。如果有边 ij，那么 r_i 应位于 r_j 的左边（或下方）.

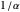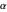为简单起见，假设所有长方形的长宽比位于 和 之间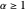，，长方形之间的间距是 。

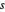给定这些输入和较小长方形的面积列表，可以定义一个函数 planFloor，它可以求出较大长方形的最小周长。

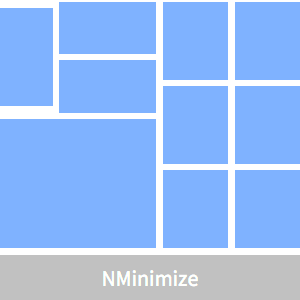
设置表示 10 个较小长方形的相对位置的图。

要求所有较小长方形的面积为 100，除了一个面积为 400 的长方形。

下面的计算将给出最佳平面规划。

显示最佳的规划。

下面的计算显示满足了面积约束条件。

比较面积是随机值情况下的布局。