最佳分配问题
求公司必须从四个发电厂向五个城市发送的电量,以便在满足城市高峰需求的同时实现利润最大化和成本最小化。
下面的例子演示了如何使用 LinearFractionalOptimization 在给定约束条件下最小化成本与利润的比率。用矩阵值变量使建模过程更简单。
令 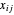 表示从电厂
表示从电厂 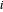 输送到城市
输送到城市 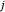 的电量。输送电力的总成本是
的电量。输送电力的总成本是 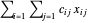 ,其中
,其中 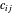 表示从电厂
表示从电厂 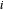 输送到城市
输送到城市 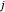 的成本。Total[m, 2] 给出矩阵
的成本。Total[m, 2] 给出矩阵 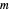 所有元素的总和。
所有元素的总和。
电力公司获得的总利润为 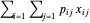 ,其中
,其中 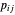 是电厂
是电厂 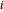 卖给城市
卖给城市 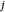 电力所获得的利润。
电力所获得的利润。
每个电厂输送的总电量为 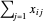 ,必须大于或等于电厂可提供的最小电量。Total[x, {2}] 给出
,必须大于或等于电厂可提供的最小电量。Total[x, {2}] 给出 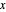 每一行的总和。
每一行的总和。
发往每个城市的总电量为 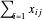 ,必须大于最低需求,小于或等于高峰需求。Total[x, 1] 给出
,必须大于最低需求,小于或等于高峰需求。Total[x, 1] 给出 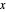 的列的总和。
的列的总和。
电厂只能为城市输送电力,不能从城市获取电力。VectorGreaterEqual 可用来表示矩阵变量 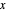 的所有元素应大于或等于零。
的所有元素应大于或等于零。
这里是从四个工厂输送一百万千瓦时 (kWh) 的电力到五个城市的成本。
以下显示了每个发电厂向每个城市出售 100 万千瓦的电力产生的利润。
各个城市高峰时期的电力需求分别为 4500 万、2 千万、3 千万、3 千万和 4 千万千瓦时,最低需求量为 500 万千瓦时。
发电厂可分别提供至少 3500 万、5 千万、4 千万 和 4 千万千瓦时的电力。
通过最小化成本与利润的比率,可以求出每个电厂输送到每个城市的最佳电量。
电力供应明细为: