꼬리가 무거운 분포에서 강력한 위치 측정값의 장점
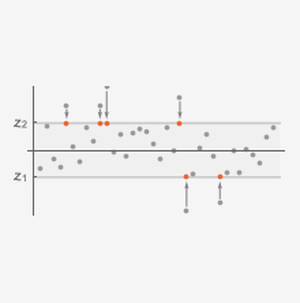
파레토 분포와 코시 분포 등과 같이 "희소한" 이벤트가 일어날 확률이 비교적 높은 분포가 있습니다. 데이터가 그런 꼬리의 무거운 분포를 따르는 경우에는, 단순 평균 등의 강력함이 아닌 위치 측정값은 잘 작동하지 않습니다. 그런 경우에는 중앙값과 이중 가중의 위치 등의 견고한 위치 측정값이 보다 적절합니다.
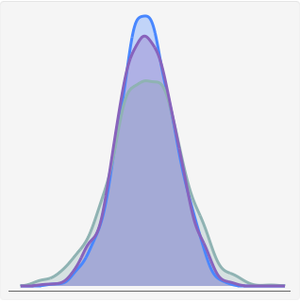
코시 분포의 확률 밀도 함수를 대응하는 NormalDistribution의 확률 밀도 함수("굵은" 꼬리가 없는)와 비교합니다.
전체 Wolfram 언어 입력 표시하기
"굵은" 꼬리를 가지는 분포의 특징 중 하나는 예를 들어 평균과 같은 모멘트는 정의되지 않는 경우가 있습니다. 그 결과, 단순 평균은 신뢰할 수 없습니다.
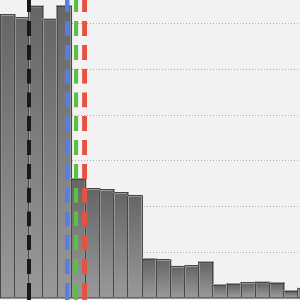
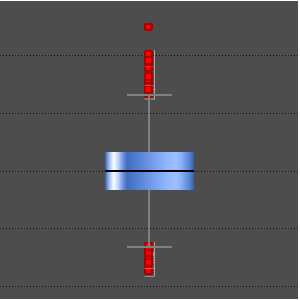
코시 분포에서 시뮬레이션이 시행된 데이터의 위치 측정값의 성능을 살펴봅니다.
평균(강력하지 않은), 중앙값(강력한), 이중 가중 위치(강력한)에서 중심 위치를 계산합니다.
견고한 위치 통계값은 "평균적"으로 꼬리가 무거운 분포의 중심 위치에 더욱 가깝습니다.
전체 Wolfram 언어 입력 표시하기
정규 분포의 데이터 내용은 이중 가중의 위치가 평균에 가깝습니다.