확장된 행렬 분포 추정하기
버전 11에서는 랜덤 행렬이 도입되었으며, 이는 지금까지의 확률과 통계의 프레임워크에 견고하게 통합되었습니다. 랜덤 행렬은, 통계, 물리, 순수 수학, 생물, 금융 등 놀라울 정도로 다양한 분야에서 사용이 가능합니다. 버전 12에서는 MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution, InverseWishartMatrixDistribution의 추정을 포함한 랜덤 행렬이 완벽하게 지원됩니다.
WishartMatrixDistribution[ν, Σ]는 자유도 매개 변수 
가 정수일 때의 공분산 행렬 
를 포함하는 다변량 가우스 분포 
개의 독립적 실현에서의 표본 공분산 분포입니다.
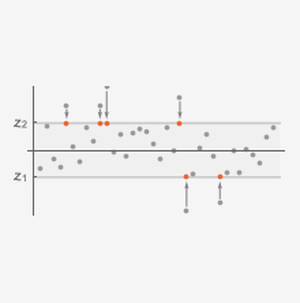
MultinormalDistribution에서 길이 n의 m 개의 무작위 표본의 시뮬레이션을 실시합니다.
각각의 목록에 대해 표본 공분산을 계산합니다.
결과는 n개의 행렬의 목록입니다.
WishartMatrixDistribution을 공분산 표본에 맞춥니다.
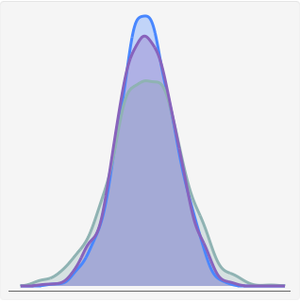
맞춘 분포의 평균과 표본 공분산의 평균을 비교합니다.
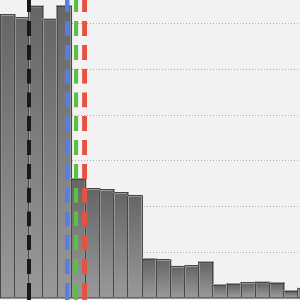
분산을 비교합니다.
WishartMatrixDistribution[ν, Σ]로의 분포에 따라 행렬 
에 대해, 역행렬 
은 InverseWishartMatrixDistribution[ν, Σ-1]로 분포에 따릅니다.
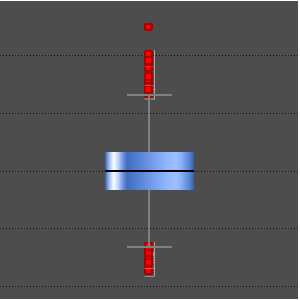
표본 공분산의 역행렬을 계산하고 InverseWishartMatrixDistribution을 맞춥니다.
추정 Wishart 행렬 분포의 공분산 행렬이 역 Wishart 모델의 역행렬인지 여부를 확인합니다.
