파레토 피칸즈 분포에서 거듭제곱 꼬리 분포 데이터 맞추기
일반화 파레토 분포(GPD)로 알려진 파레토 피칸즈 분포는 극단적인 차수 통계를 조사하기 위해 도입된 것으로, 높은 임계값을 초과하는 이벤트를 나타내는 데 자주 사용됩니다. 파레토 피칸즈 분포는 보험, 수문학, 기후학에 응용됩니다.
파레토 피칸즈 분포는 거듭제곱 꼬리 분포의 초과를 모델링하는 데 사용할 수 있습니다. 이러한 분포의 대부분은 CauchyDistribution, DagumDistribution, LogGammaDistribution, ParetoDistribution, StudentTDistribution 등과 같은 Wolfram 언어로 존재합니다.
이 분포의 높은 모멘트는 존재하지 않습니다.
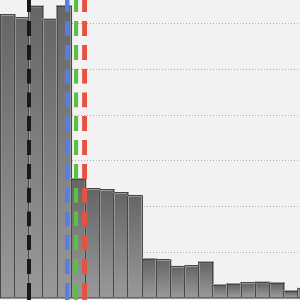
히스토그램은 표본이 긴 꼬리를 가지는 것을 나타냅니다.
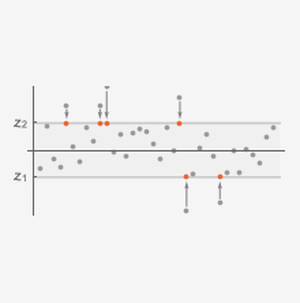
꼬리에서 큰 값을 제외하여 데이터를 잘라냅니다.
꼬리의 데이터를 파레토 피칸즈 분포에 맞춥니다.
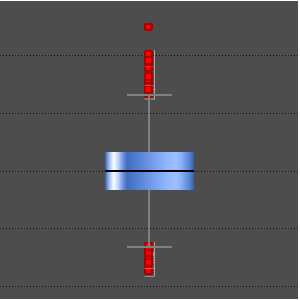
분위수 플롯에서 적합도를 확인합니다.
적합도를 검정합니다.
재미있는 의사 사실에, 표준 파레토-피칸즈 분포는 확률적 질서 분포라고 하는 것이 있습니다. 즉, 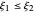 에 대한 누적 분포 함수도 모든
에 대한 누적 분포 함수도 모든 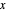 에 대하여 질서 분포
에 대하여 질서 분포 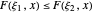 입니다.
입니다.
전체 Wolfram 언어 입력 표시하기