Estimación extendida de distribuciones matriciales
La versión 11 introdujo las matrices aleatorias, las cuales habían sido integradas firmemente con el marco de probabilidad y estadística existente. Las matrices aleatorias se aplican en una sorprendente variedad de campos, incluyendo estadística, física, matemática pura, biología y finanzas, entre otros. La versión 12 completa el soporte para matrices aleatorias con estimación para MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution e InverseWishartMatrixDistribution.
WishartMatrixDistribution[ν, Σ] es la distribución de la covarianza de muestra de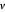 
realizaciones independientes de una distribución gaussiana multivariable con matriz de covarianza 
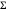cuando el parámetro de grados de libertad 
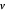es un entero.
Modele m muestras aleatorias de longitud n de una MultinormalDistribution.
Calcule la covarianza de muestra para cada lista.
El resultado es una lista de n matrices.
Ajuste WishartMatrixDistribution a la muestra de covarianza.
Compare la media de la distribución ajustada con la media de las covarianzas de muestra.
Compare las varianzas.
Para una matriz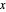 
distribuida como WishartMatrixDistribution[ν, Σ], el inverso 
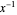se distribuye como InverseWishartMatrixDistribution[ν, Σ-1].
Calcule el inverso de las covarianzas de muestra y ajuste un InverseWishartMatrixDistribution.
Compruebe si la matriz de covarianza de la distribución de matriz Wishart estimada es la inversa del modelo Wishart inverso.
