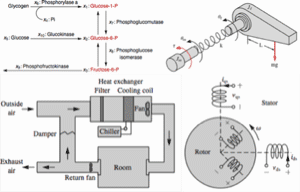
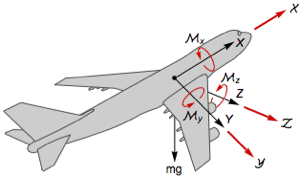
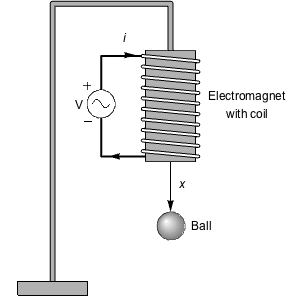
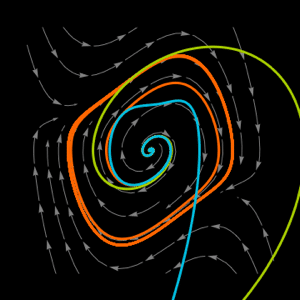
Affine Nonlinear Systems
Affine systems are nonlinear systems that are linear in the input. They can be specified in multiple ways and can also be converted to other systems models.
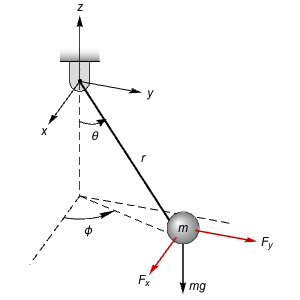
A system specified using an ODE.
| In[1]:= | X |
| Out[1]= | 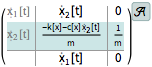 |
A system specified using its components.
| In[2]:= | 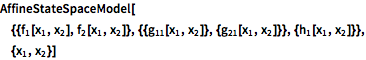 X |
| Out[2]= | 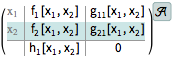 |
Systems obtained from other systems models.
| In[3]:= | 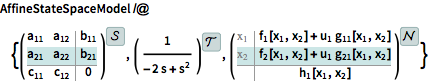 X |
| Out[3]= | 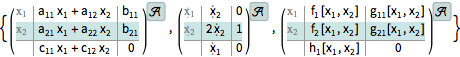 |
A NonlinearStateSpaceModel that is not input linear is approximated.
| In[4]:= | 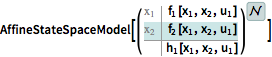 X |
| Out[4]= | 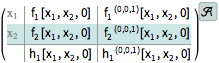 |
A linear AffineStateSpaceModel is exactly converted to linear systems models.
| In[5]:= | 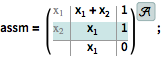 X |
| In[6]:= | X |
| Out[6]= | 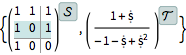 |
In general, affine models are approximated during conversion to linear systems models.
| In[7]:= | 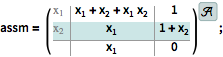 X |
| In[8]:= | X |
| Out[8]= | 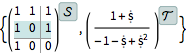 |
The conversion to a NonlinearStateSpaceModel is exact.
| In[9]:= | 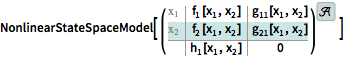 X |
| Out[9]= | 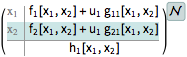 |