Examples of Affine Systems 

The control inputs appear linearly in a wide variety of applications, and thus many systems can be modeled effectively using AffineStateSpaceModel.

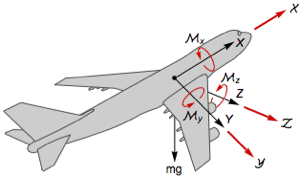
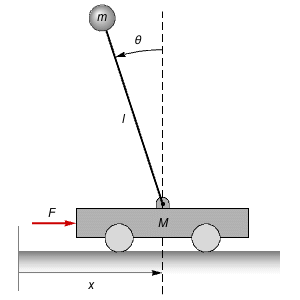
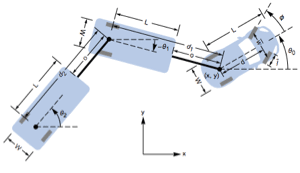
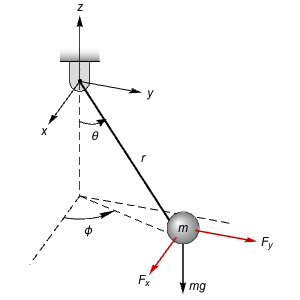
The model of a flexible joint. »

In[1]:=

X AffineStateSpaceModel[ {{Subscript[\[Theta], dl][ t], (-g L M Sin[Subscript[\[Theta], l][t]] - k Subscript[\[Theta], l][t] + k Subscript[\[Theta], m][t])/ Subscript[J, l], Subscript[\[Theta], dm][t], ( k Subscript[\[Theta], l][t] - k Subscript[\[Theta], m][t])/ Subscript[J, m]}, {{ 0 }, {0 }, {0 }, {1/Subscript[J, m] }}, {Subscript[\[Theta], l][t]}, {{ 0 }}}, {Subscript[\[Theta], l][t], Subscript[\[Theta], dl][t], Subscript[\[Theta], m][t], Subscript[\[Theta], dm][t]}, {{\[Tau][t], 0}}, {Automatic}, t , SamplingPeriod -> None] ;

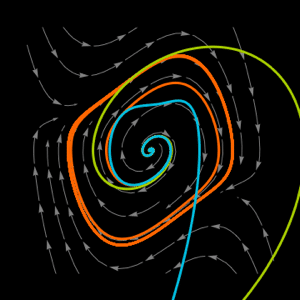
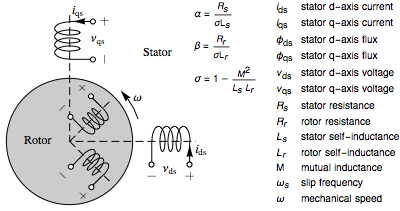
A model for an induction motor in d-q (direct-quadrature) rotating coordinates with inputs 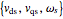as inputs. »

In[2]:=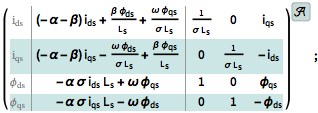

X AffineStateSpaceModel[ {{(-\[Alpha] - \[Beta]) Subscript[i, ds] + (\[Beta] Subscript[\[Phi], ds])/Subscript[L, s] + (\[Omega] Subscript[\[Phi], qs])/(\[Sigma] Subscript[L, s]), (-\[Alpha] - \[Beta]) Subscript[i, qs] - (\[Omega] Subscript[\[Phi], ds])/(\[Sigma] Subscript[L, s]) + (\[Beta] Subscript[\[Phi], qs])/Subscript[L, s], -\[Alpha] \[Sigma] Subscript[i, ds] Subscript[L, s] + \[Omega] Subscript[\[Phi], qs], -\[Alpha] \[Sigma] Subscript[ i, qs] Subscript[L, s] - \[Omega] Subscript[\[Phi], ds]}, {{ 1/(\[Sigma] Subscript[L, s]), 0, Subscript[i, qs] }, {0, 1/(\[Sigma] Subscript[L, s]), -Subscript[i, ds] }, {1, 0, Subscript[\[Phi], qs] }, {0, 1, -Subscript[\[Phi], ds] }}}, {Subscript[i, ds], Subscript[i, qs], Subscript[\[Phi], ds], Subscript[\[Phi], qs]}, Automatic, {Automatic, Automatic, Automatic, Automatic}, Automatic , SamplingPeriod -> None , SystemsModelLabels -> {None, {}, None}] ;

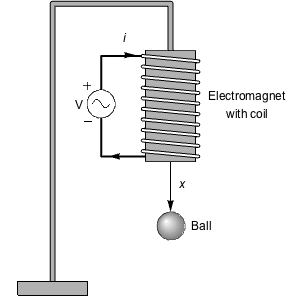
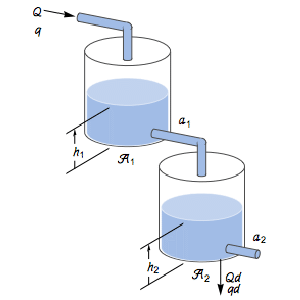
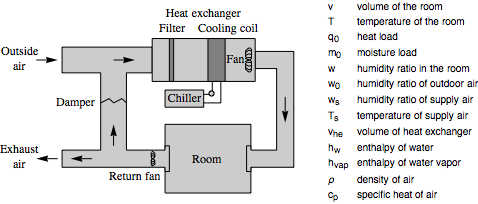
A model for a room cooling system with the air and water flow as inputs. »

In[3]:=

X AffineStateSpaceModel[ {{(-Subscript[h, vap] Subscript[m, 0] + Subscript[q, 0])/(v \[Rho] Subscript[c, p]), Subscript[m, 0]/( v \[Rho]), 0}, {{ (60 (-T + Subscript[T, s]))/v - ( 60 Subscript[h, vap] (-w + Subscript[w, s]))/(v Subscript[c, p]), 0 }, {(60 (-w + Subscript[w, s]))/v, 0 }, {(15 (-T + Subscript[T, 0]))/Subscript[v, he] + ( 60 (T - Subscript[T, s]))/Subscript[v, he] - ( 60 Subscript[h, w] ((3 w)/4 + Subscript[w, 0]/4 - Subscript[w, s]))/( Subscript[c, p] Subscript[v, he]), -( 6000/(\[Rho] Subscript[c, p] Subscript[v, he])) }}, {T, Subscript[ T, s]}, {{ 0, 0 }, {0, 0 }}}, {{T, 23}, {w, 0.0097562}, {Subscript[T, s], 14}}, {{Subscript[u, 1], 77.4218}, {Subscript[u, 2], 6.07984}}, {Automatic, Automatic}, Automatic , SamplingPeriod -> None] ;

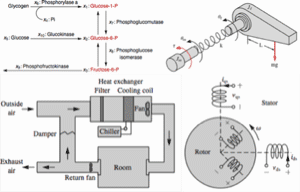
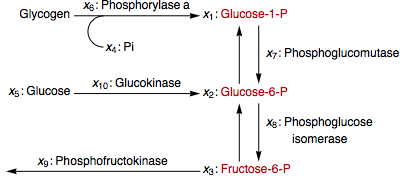
The model of a glycolytic-glycogenolytic pathway where the rates of metabolite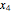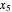s , , and are taken as the inputs, an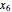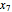d , , , and 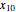are kept constant. »

In[4]:=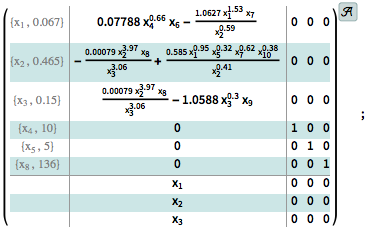

X AffineStateSpaceModel[ {{0.07788 \!\(\*SubsuperscriptBox[\(x\), \(4\), \(0.66`\)]\) Subscript[x, 6] - ( 1.0627 \!\(\*SubsuperscriptBox[\(x\), \(1\), \(1.53`\)]\) Subscript[x, 7])/ \!\(\*SubsuperscriptBox[\(x\), \(2\), \(0.59`\)]\), -((0.00079 \!\(\*SubsuperscriptBox[\(x\), \(2\), \(3.97`\)]\) Subscript[x, 8])/ \!\(\*SubsuperscriptBox[\(x\), \(3\), \(3.06`\)]\)) + (0.585 \!\(\*SubsuperscriptBox[\(x\), \(1\), \(0.95`\)]\) \!\(\*SubsuperscriptBox[\(x\), \(5\), \(0.32`\)]\) \!\(\*SubsuperscriptBox[\(x\), \(7\), \(0.62`\)]\) \!\(\*SubsuperscriptBox[\(x\), \(10\), \(0.38`\)]\))/ \!\(\*SubsuperscriptBox[\(x\), \(2\), \(0.41`\)]\), (0.00079 \!\(\*SubsuperscriptBox[\(x\), \(2\), \(3.97`\)]\) Subscript[x, 8])/ \!\(\*SubsuperscriptBox[\(x\), \(3\), \(3.06`\)]\) - 1.0588 \!\(\*SubsuperscriptBox[\(x\), \(3\), \(0.3`\)]\) Subscript[x, 9], 0, 0, 0}, {{ 0, 0, 0 }, {0, 0, 0 }, {0, 0, 0 }, {1, 0, 0 }, {0, 1, 0 }, {0, 0, 1 }}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, {{ 0, 0, 0 }, {0, 0, 0 }, {0, 0, 0 }}}, {{Subscript[x, 1], 0.067}, {Subscript[x, 2], 0.465}, {Subscript[x, 3], 0.15}, {Subscript[x, 4], 10}, {Subscript[ x, 5], 5}, {Subscript[x, 8], 136}}, Automatic, {Automatic, Automatic, Automatic}, Automatic , SamplingPeriod -> None] ;