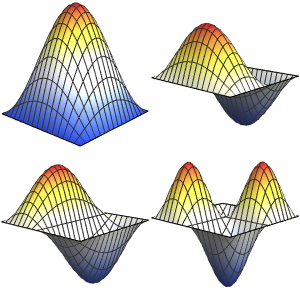
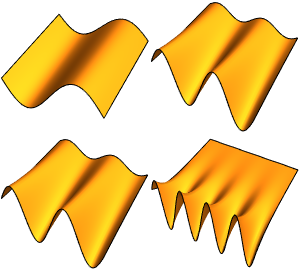
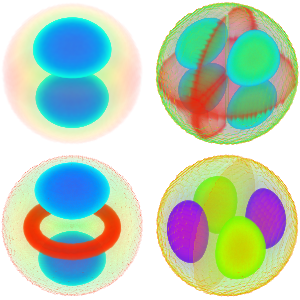
記号固有値を計算する

1Dのラプラス演算子を指定する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

同次ディリクレ境界条件を指定する．

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

区間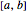において5つの最小の固有値に対する式を求める．

In[3]:=

DEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, a, b}, 5]

Out[3]=

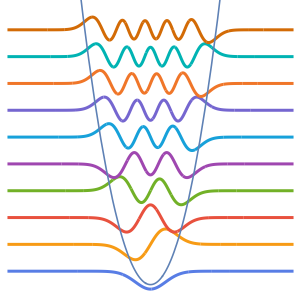
エアリー(Airy)演算子を指定する．

In[4]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}] + x u[x];

5つの最小の固有値と，それに対応する固有関数を求める．

In[5]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 1}, 5];

この固有値は，超越方程式の根である．

In[6]:=

vals[[1]] // TraditionalForm

Out[6]//TraditionalForm=

超越固有値を高精度で計算する．

In[7]:=

N[vals[[1]], 500] // TraditionalForm

Out[7]//TraditionalForm=

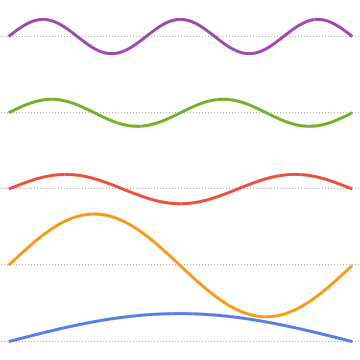
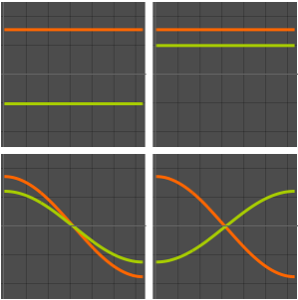
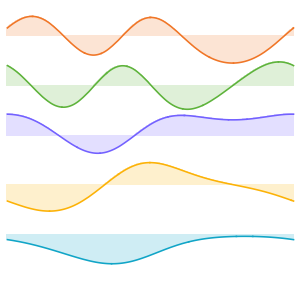
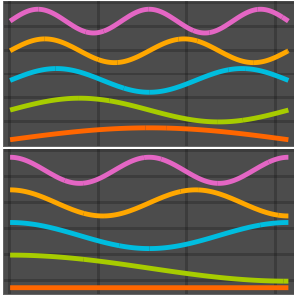
固有関数を可視化する．

In[8]:=

Plot[Evaluate[funs + Range[5]], {x, 0, 1}, ImageSize -> Medium, PlotTheme -> {"Business", "Bare"}, AspectRatio -> 1]

Out[8]=