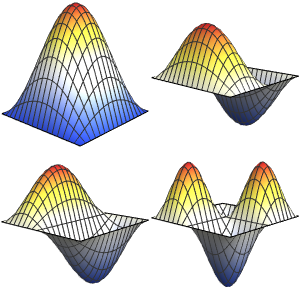
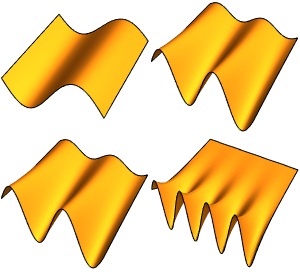
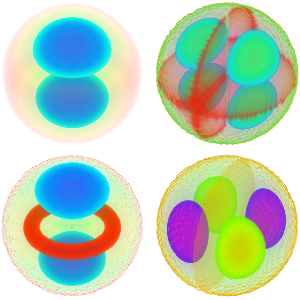
计算符号特征值

设定一维拉普拉斯算子.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

设定一个齐次狄利克雷边界条件.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

在区间 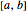上求最小的五个特征值的符号表达式.

In[3]:=

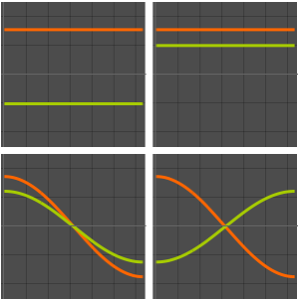
DEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, a, b}, 5]

Out[3]=

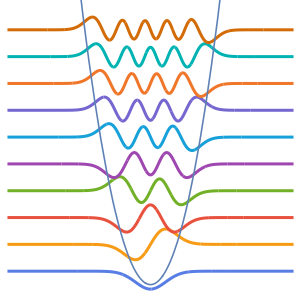
设定一个爱里（Airy）算子.

In[4]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}] + x u[x];

求最小的五个特征值及相应的特征函数.

In[5]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 1}, 5];

特征值是一个超越方程的根.

In[6]:=

vals[[1]] // TraditionalForm

Out[6]//TraditionalForm=

计算高精度的超越特征值.

In[7]:=

N[vals[[1]], 500] // TraditionalForm

Out[7]//TraditionalForm=

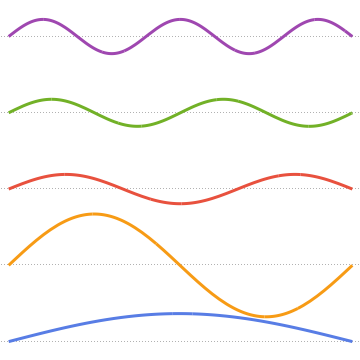
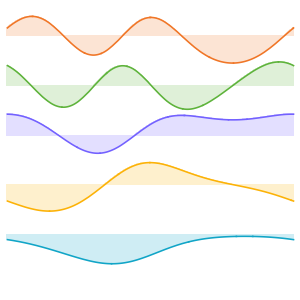
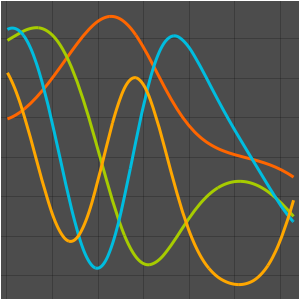
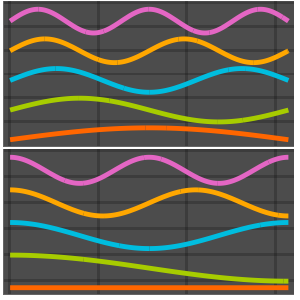
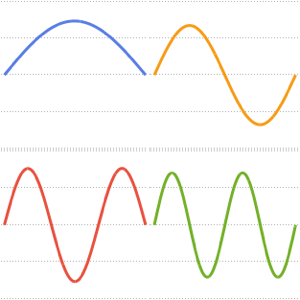
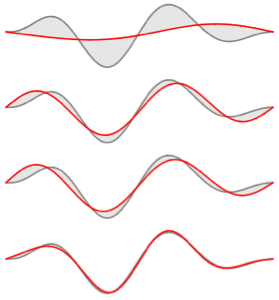
可视化特征函数.

In[8]:=

Plot[Evaluate[funs + Range[5]], {x, 0, 1}, ImageSize -> Medium, PlotTheme -> {"Business", "Bare"}, AspectRatio -> 1]

Out[8]=