Wolfram言語™

シュレーディンガー(Schrödinger)演算子のスペクトルを求める

一次元領域上でシュレーディンガー方程式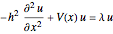 の固有値問題を解く．

制約条件のないシュレーディンガー演算子を指定する．

In[1]:=

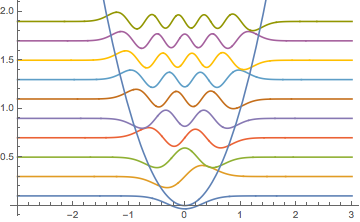
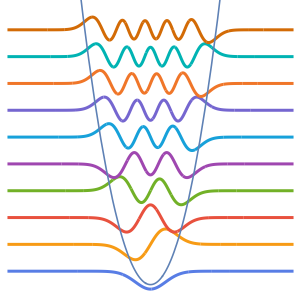
h = 1/10; V[x_] := x^2 \[ScriptCapitalL] = -h^2*u''[x] + V[x]*u[x];

調整されたメッシュ上で，固有値と固有関数を小さい方から10個求める．

In[2]:=

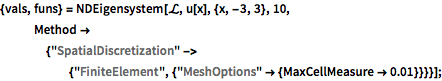
{vals, funs} = NDEigensystem[\[ScriptCapitalL], u[x], {x, -3, 3}, 10, Method -> {"SpatialDiscretization" -> {"FiniteElement", \ {"MeshOptions" -> {MaxCellMeasure -> 0.01}}}}];

固有値を調べる．

In[3]:=

vals

Out[3]=

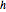でスケールされ，それぞれ対応する固有値でオフセットされた固有関数を可視化する．

In[4]:=

Show[Plot[Evaluate[h*funs + vals], {x, -3, 3}], Plot[V[x], {x, -3, 3}], PlotRange -> {{-3, 3}, {0, 2}}, AxesOrigin -> {-3, 0}, ImageSize -> Medium]

Out[4]=