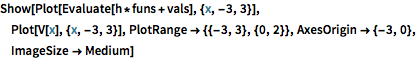Wolfram 语言™

求薛定谔算子的谱

在一个一维区域上求解薛定谔方程 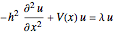的特征值问题.

设定一个无约束的薛定谔算子.

In[1]:=

h = 1/10; V[x_] := x^2 \[ScriptCapitalL] = -h^2*u''[x] + V[x]*u[x];

在细化网格上找出最小的 10 个特征值和特征函数.

In[2]:=

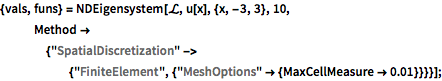
{vals, funs} = NDEigensystem[\[ScriptCapitalL], u[x], {x, -3, 3}, 10, Method -> {"SpatialDiscretization" -> {"FiniteElement", \ {"MeshOptions" -> {MaxCellMeasure -> 0.01}}}}];

查看特征值.

In[3]:=

vals

Out[3]=

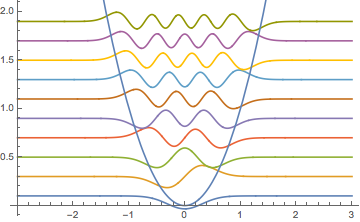
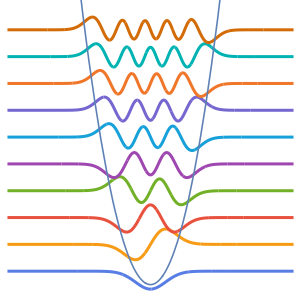
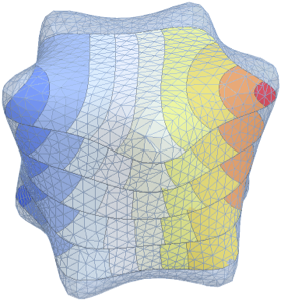
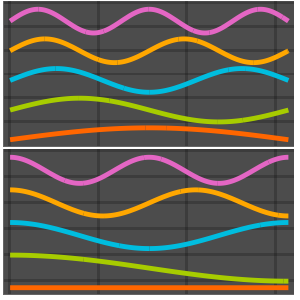
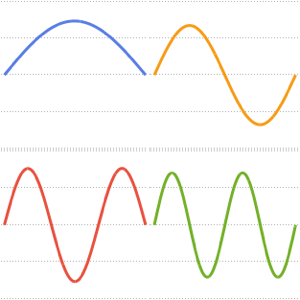
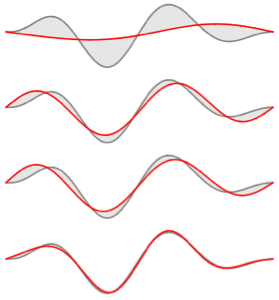
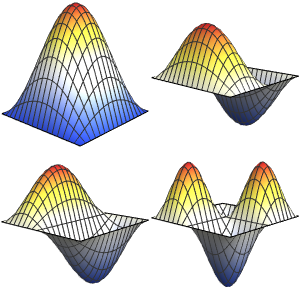
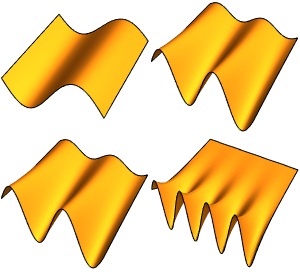
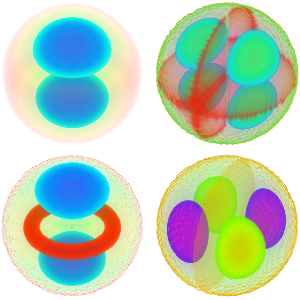
可视化特征函数. 特征函数按 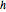标度，并按各自的特征值做了平移.

In[4]:=

Show[Plot[Evaluate[h*funs + vals], {x, -3, 3}], Plot[V[x], {x, -3, 3}], PlotRange -> {{-3, 3}, {0, 2}}, AxesOrigin -> {-3, 0}, ImageSize -> Medium]

Out[4]=