Определим спектр оператора Шредингера

Найдем собственные значения для уравнения Шредингера 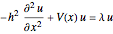в 1-мерном пространстве.

Укажем неограниченный оператор Шредингера.

In[1]:=

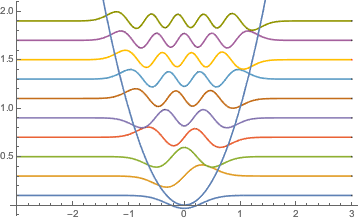
h = 1/10; V[x_] := x^2 \[ScriptCapitalL] = -h^2*u''[x] + V[x]*u[x];

Найдем 10 наименьших собственных значений и собственных функций на сетке.

In[2]:=

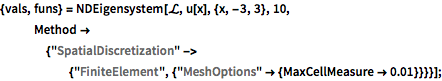
{vals, funs} = NDEigensystem[\[ScriptCapitalL], u[x], {x, -3, 3}, 10, Method -> {"SpatialDiscretization" -> {"FiniteElement", \ {"MeshOptions" -> {MaxCellMeasure -> 0.01}}}}];

Рассмотрим полученные собственные значения.

In[3]:=

vals

Out[3]=

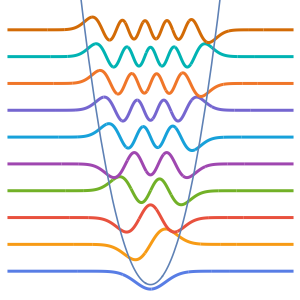
Визуализируем собственные функции с масштабом h и в соответствии с полученными собственными значениями.

In[4]:=

Show[Plot[Evaluate[h*funs + vals], {x, -3, 3}], Plot[V[x], {x, -3, 3}], PlotRange -> {{-3, 3}, {0, 2}}, AxesOrigin -> {-3, 0}, ImageSize -> Medium]

Out[4]=