Wolfram Mathematica

Solve the Eigenproblem of a Constrained Laplacian

Find the four smallest eigenvalues and eigenfunctions of a Laplacian equation 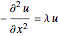over a 1D region constrained by homogeneous Dirichlet boundary conditions.

Specify a Laplacian.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Set up a Dirichlet boundary condition.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

Numerically find the eigenvalues.

In[3]:=

NDEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4]

Out[3]=

Numerically find the eigenvalues and eigenfunctions.

In[4]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4];

Inspect the eigenvalues.

In[5]:=

vals

Out[5]=

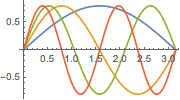
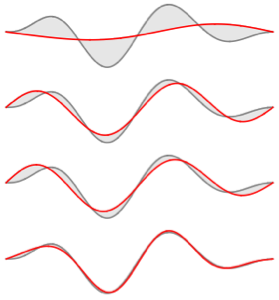
Visualize the eigenfunctions.

In[6]:=

Plot[Evaluate[funs], {x, 0, \[Pi]}]

Out[6]=