Étudiez un système de Sturm-Liouville avec des conditions aux limites antipériodiques

Trouvez les cinq plus petites valeurs propres et fonctions propres antipériodiques relationnelles d'un opérateur de Sturm-Liouville.

Spécifiez un opérateur de Sturm-Liouville.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

Spécifiez une condition aux limites antipériodique relationnelle.

In[2]:=

\[ScriptCapitalB] = PeriodicBoundaryCondition[-2 u[x], x == 2 \[Pi], TranslationTransform[{-2 \[Pi]}]];

Trouvez les cinq plus petits valeurs et fonctions propres.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

Inspectez les valeurs propres.

In[4]:=

vals

Out[4]=

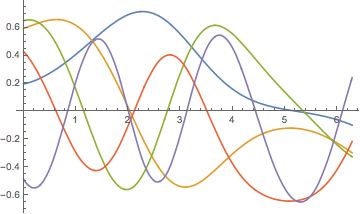
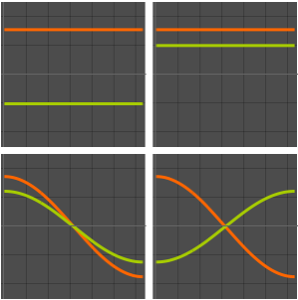
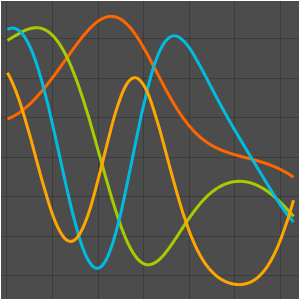
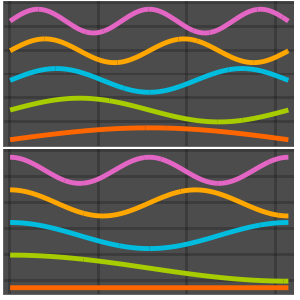
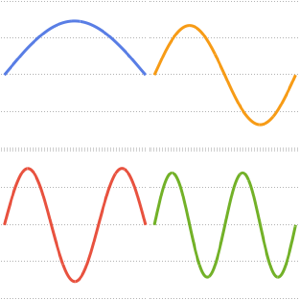
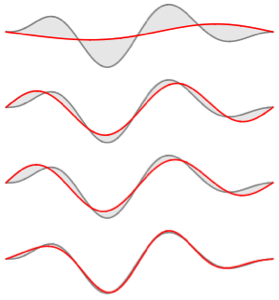
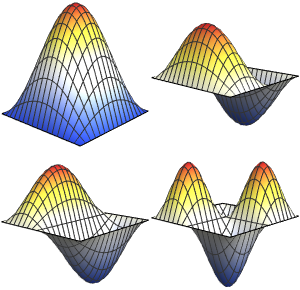
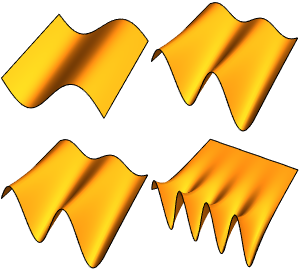
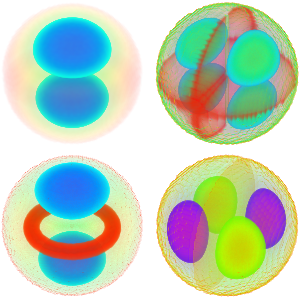
Visualisez les fonctions propres.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=