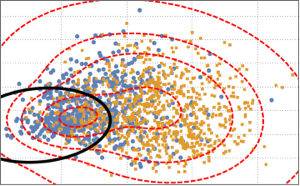
Modélisation des réseaux sociaux : Nouveautés de Wolfram Language 11

Modélisation des réseaux sociaux

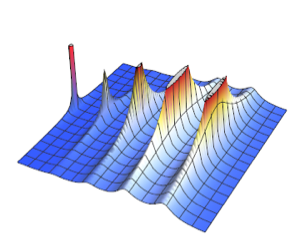
La loi de Gompertz décalée est la loi du maximum de variables aléatoires indépendantes exponentielles et à valeurs extrêmes. Cette loi peut être utilisée pour modéliser la croissance et le déclin de l'intérêt pour les réseaux sociaux. La fonction de distribution cumulative (CDF) de la loi de Gompertz décalée prend la forme suivante.

In[1]:=

CDF[ShiftedGompertzDistribution[\[Lambda], \[Xi]], x]

Out[1]=

Les chiffres hebdomadaires de l'intérêt pour Facebook sont tirés de Google Trends.

In[2]:=

ts = TemporalData[TimeSeries, {CompressedData["
1:eJyFz2tPwjAUBmDA+7wRNCpeQBTRiAGvXLoNYYytPW03QHSybiYav/tX/Ume
GRO/mPg0p+l72pykpbeP8VsmlUqlsT5xS/8n82smM/Nt9sdcYv4vC2gxoWlL
mqYto5WVVbS2tp7N5nK5jY3N7Z2tnXx+d3dvbx/XQbFwUCgUi4eHpdLRcbl8
UjmtnJ1XqxeoVqvV65dX9cvrZvP2pnHXaLUbjWaLIJMYuk4MwzTNTue+1+1a
qO9a9qA/cPq2PRg4ILnLgHPGgLkuABfSdRyHUs5AAghvyD3peb4U+IhLJoCB
NxLUk0JwgXcCRNIT2AYpPS4YByo5cGBsFL+oOFaRCqP4/VWpOFQqCKbhVEXh
9BmFKopjTFEQBs9PweRxNHkYj/yh7/ueEHI8xDGAg7AAqMsodRw3OTP2HWxK
XfyFbVl2z+p2kGn1jATRSZsQXW+RNkpSmxjkC/7xXxc=
"], {
TemporalData`DateSpecification[{2006, 8, 26, 0, 0, 0.}, {
      2015, 7, 11, 0, 0, 0.}, {1, "Week"}]}, 1, {"Continuous", 1}, {
    "Discrete", 1}, 1, {
    ValueDimensions -> 1, DateFunction -> Automatic, 
     ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}},
    True, 314.1];

Afficher l'entrée complète de Wolfram Language

In[3]:=

DateListPlot[ts, ImageSize -> Medium, PlotTheme -> "Detailed", 
 Filling -> Axis]

Out[3]=

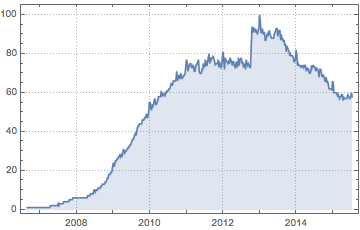
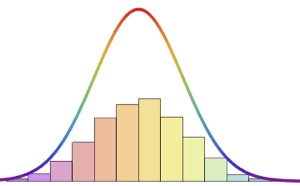
Ajustement des données à une loi de Gompertz tronquée et décalée.

In[4]:=

rawcounts = ts["Values"];
length = Length[rawcounts];
x = Range[length] - 0.5;
wdata = WeightedData[x, rawcounts];

In[5]:=

edist = EstimatedDistribution[wdata, 
  TruncatedDistribution[{0, length}, 
   ShiftedGompertzDistribution[\[Lambda], \[Xi]]], {{\[Lambda], 
    1}, {\[Xi], 6}}]

Out[5]=

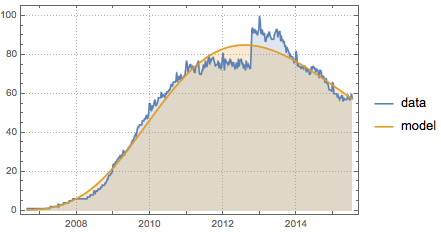
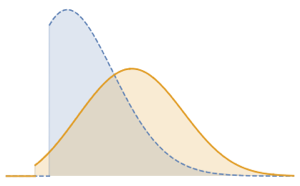
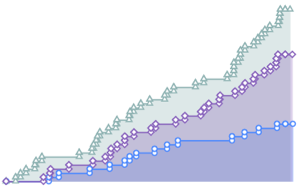
Comparez les prédictions du modèle aux données.

Afficher l'entrée complète de Wolfram Language

In[6]:=

counts = Total[rawcounts] PDF[edist , x];
DateListPlot[{rawcounts, counts}, {ts["FirstDate"], Automatic, 
  "Week"}, Filling -> Axis, PlotLegends -> {"data", "model"}, 
 ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[6]=