Davantage de simplification automatique pour les lois transformées : Nouveautés de Wolfram Language 11

‹›

Davantage de simplification automatique pour les lois transformées

La version 11 ajoute des règles de simplification plus automatiques pour les lois transformées.

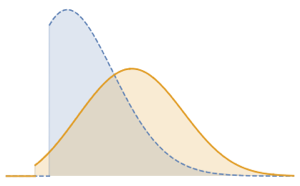
La puissance d'une variable aléatoire uniformément distribuée est une loi bêta.

In[1]:=

TransformedDistribution[X^a, X \[Distributed] UniformDistribution[]]

Out[1]=

Le rapport de variables aléatoires indépendantes à loi exponentielle satisfait la loi de Pareto.

In[2]:=

TransformedDistribution[
 X/Y, {X \[Distributed] ExponentialDistribution[b], 
  Y \[Distributed] ExponentialDistribution[a]}]

Out[2]=

Le carré inverse d'une variable aléatoire normalement distribuée est la loi de Lévy.

In[3]:=

TransformedDistribution[X^(-2), 
 X \[Distributed] NormalDistribution[0, s]]

Out[3]=

D'autres exemples peuvent être trouvés dans le tableau suivant.

Afficher l'entrée complète de Wolfram Language

In[4]:=

SetAttributes[fun, HoldFirst];
fun[x_] := {HoldForm[x], x};
Grid[Map[Style[#, ScriptLevel -> 0] &, 
   Join[{{"Transformed Distribution", "Simplified Distribution"}}, {
     fun[TransformedDistribution[
       Min[Subscript[X, 1], Subscript[X, 
        2]], {Subscript[X, 1] \[Distributed] 
         BernoulliDistribution[Subscript[p, 1]], 
        Subscript[X, 2] \[Distributed] 
         BernoulliDistribution[Subscript[p, 2]]}]], 
     fun[TransformedDistribution[1/X, 
       X \[Distributed] LogLogisticDistribution[\[Gamma], \[Sigma]]]],
      fun[TransformedDistribution[k*X, 
       X \[Distributed] ChiDistribution[\[Nu]]]], 
     fun[TransformedDistribution[1/X, 
       X \[Distributed] BetaPrimeDistribution[a, b]]], 
     fun[TransformedDistribution[k*Exp[-X], 
       X \[Distributed] ExponentialDistribution[a]]], 
     fun[TransformedDistribution[-Log[X], 
       X \[Distributed] PowerDistribution[1, a]]], 
     fun[TransformedDistribution[c*X, 
       X \[Distributed] ChiSquareDistribution[a]]], 
     fun[TransformedDistribution[1 + X, 
       X \[Distributed] ExponentialDistribution[a]]], 
     fun[TransformedDistribution[
       Sqrt[X*Y], {X \[Distributed] ExponentialDistribution[m], 
        Y \[Distributed] GammaDistribution[a, b]}]], 
     fun[TransformedDistribution[Log[X]/2, 
       X \[Distributed] FRatioDistribution[n, m]]], 
     fun[TransformedDistribution[R^2, 
       R \[Distributed] RiceDistribution[\[Nu], 1]]]
     }], {2}], Dividers -> All, Spacings -> {4, 2}, 
  Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> 
      Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, 
  BaseStyle -> {FontFamily -> Times, FontSize -> 13}, 
  Alignment -> {Center, Center}] // TraditionalForm

Out[4]//TraditionalForm=