Analyse des données des maladies cardiovasculaires: Nouveautés de Wolfram Language 11

Analyse des données des maladies cardiovasculaires

L'analyse des données est un processus d'extraction, de présentation et de modélisation basée sur des informations extraites de sources premières. Dans cet exemple, un flux de travail de l'analyse des données effectuée en Wolfram Language est présenté. L'ensemble de données utilisé ici provient de UCI Machine Learning Repository, composé de données de diagnostic des maladies cardiovasculaires de 1541 patients.

Importez des données de diagnostic des maladies cardiovasculaires et analysez-les de sorte que les lignes correspondent aux différents patients et les colonnes correspondent à des attributs différents.

In[1]:=

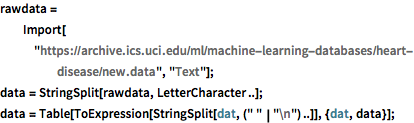
rawdata = 
  Import["https://archive.ics.uci.edu/ml/machine-learning-databases/\
heart-disease/new.data", "Text"];
data = StringSplit[rawdata, LetterCharacter ..];
data = Table[
   ToExpression[StringSplit[dat, (" " | "\n") ..]], {dat, data}];

Extrayez les attributs pertinents dans "étiquettes" et "caractéristiques". Les valeurs stockées dans des «étiquettes» sont comprises entre 0 et 1, correspondant à la présence et à l'absence de maladie cardiovasculaire, respectivement.

In[2]:=

labels = Unitize[data[[All, 58]]];
features = 
  data[[All, {3, 4, 9, 10, 12, 16, 19, 32, 38, 40, 41, 44, 51}]];

In[3]:=

Take[labels, 10]

Out[3]=

Pour chaque patient, le vecteur caractéristique est une liste de valeurs numériques. Toutefois, les données ne sont pas complètes et a les champs manquants enregistrés comme 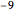-9.

In[4]:=

features[[-3]]

Out[4]=

Remplacez les valeurs manquantes par la moyenne des données disponibles dans l'attribut correspondant, puis visualisez la corrélation entre les différents attributs.

In[5]:=

features = Transpose[Table[
    N[attribute /. {-9 -> Mean[N[DeleteCases[attribute, -9]]]}]
    , {attribute, Transpose[features]}]];
cormat = Correlation[features];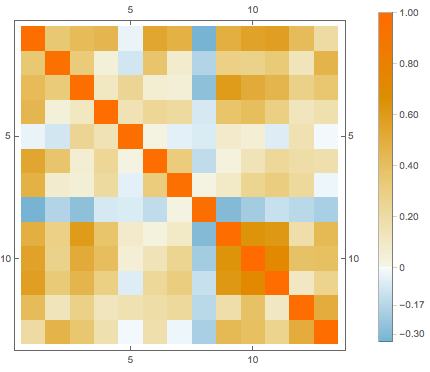

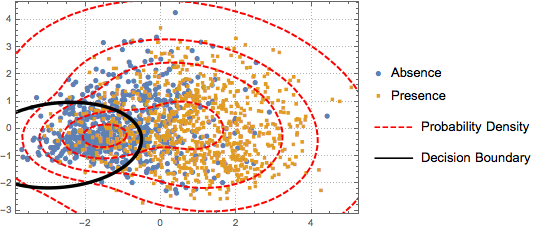
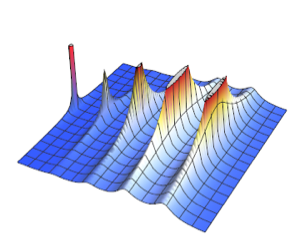
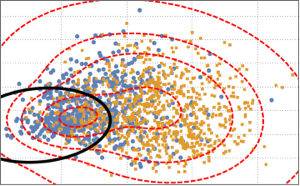
Montrer l'entrée complète de Wolfram Language

In[6]:=

MatrixPlot[cormat, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[6]=

Pour visualiser la distribution des données, l'APC est effectuée pour extraire les deux premières composantes principales, puis les données projetées sont présentées sur un diagramme de dispersion.

In[7]:=

pcs2 = Take[PrincipalComponents[features, Method -> "Correlation"], 
   All, 2];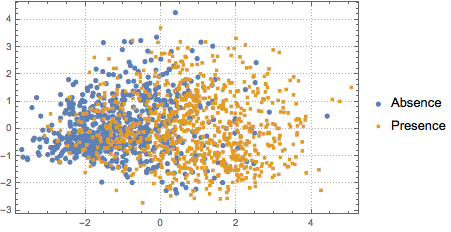

Montrer l'entrée complète de Wolfram Language

In[8]:=

splot = With[{ind = Pick[Range[Length[pcs2]], labels, 0]},
  ListPlot[{pcs2[[ind]], Delete[pcs2, Transpose[{ind}]]}, 
   ImageSize -> Medium, PlotTheme -> "Detailed", 
   PlotMarkers -> Automatic, PlotLegends -> {"Absence", "Presence"}]
  ]

Out[8]=

Pour distinguer les deux catégories, les données de projection sont ajustées sur un modèle de mélange gaussien à deux composantes.

In[9]:=

edist = EstimatedDistribution[pcs2, 
   MixtureDistribution[{p1, 
     p2}, {BinormalDistribution[{m11, m12}, {s11, s12}, r1], 
     BinormalDistribution[{m21, m22}, {s21, s22}, r2]}]];

Se basant sur le modèle de mélange, tracez la limite de décision (courbe noire) et les contours de densité de probabilité (courbe rouge) du modèle de mélange et montrez-les ainsi que le diagramme de dispersion. La première composante du mélange gaussien a une probabilité élevée à l'intérieur de la limite de décision.

Montrer l'entrée complète de Wolfram Language

In[10]:=

Module[{p = edist[[1, 1]], dist1 = edist[[2, 1]], 
  dist2 = edist[[2, 2]], prob},
 prob[x_, y_] := 
  p PDF[dist1, {x, 
      y}]/(p PDF[dist1, {x, y}] + (1 - p) PDF[dist2, {x, y}]);
 Show[splot, 
  ContourPlot[
   PDF[edist, {x, y}] == {0.1, 0.05, 0.0125, 0.003, 0.0001}, {x, -4, 
    6}, {y, -4, 6}, ImageSize -> Medium, PlotTheme -> "Detailed", 
   ContourStyle -> Red, PlotPoints -> 25], 
  ContourPlot[prob[x, y] == 1/2, {x, -4, 6}, {y, -4, 6}, 
   ImageSize -> Medium, PlotTheme -> "Detailed", 
   ContourStyle -> {Thick, Black}, PlotPoints -> 25]]
 ]

Out[10]=