Wolfram Language™

Renvois logarithmiques des prix des actions

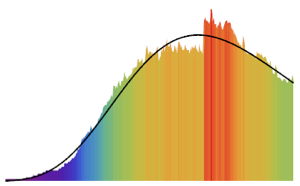
Les cours des actions modélisées avec le mouvement brownien géométrique (dans le modèle classique Black–Scholes) sont supposés être distribués normalement dans leurs renvois logarithmiques. Ici, cette hypothèse est examinée avec les cours des actions de cinq sociétés : Google, Microsoft, Facebook, Apple et Intel.

Récupérez les cours des actions en 2015 avec FinancialData.

In[1]:=

symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"}; prices = Table[ FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, symbols}];

Calculez les renvois logarithmiques.

In[2]:=

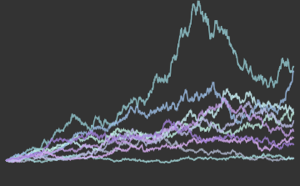
logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

Filtrez les renvois logarithmiques avec une ARCHProcess d'ordre 1.

In[3]:=

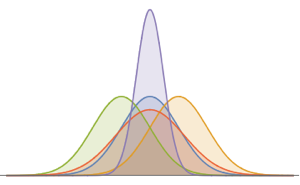
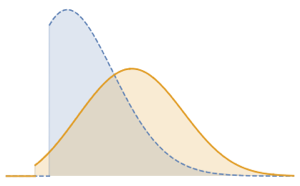
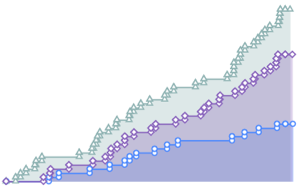
fdata = Table[ {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]]; MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2] , {lr, logreturn}]; fdata = Transpose[fdata];

Comparez les données filtrées de chaque action avec la loi normale en utilisant QuantilePlot. Pour les cinq sociétés, les queues s'écartent de la normale.

In[4]:=

MapThread[ QuantilePlot[#1, PlotLabel -> #2, PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

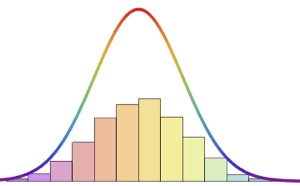
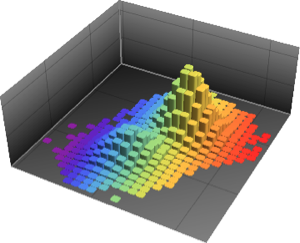
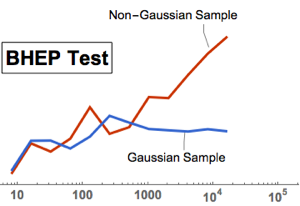
Effectuez un test de normalité multivariée avec BaringhausHenzeTest (BHEP). L'hypothèse de normalité est clairement rejetée.

In[5]:=

htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

Ajustez les données filtrées avec MultinormalDistribution et MultivariateTDistribution.

In[8]:=

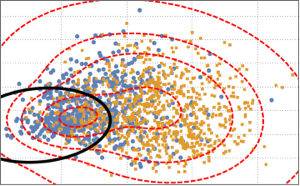
multiN = EstimatedDistribution[fdata, MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

multiT = EstimatedDistribution[fdata, MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

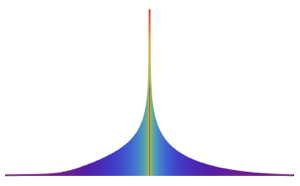
Calculez l'AIC pour les deux distributions. Le modèle de MultivariateTDistribution a une valeur inférieure.

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=